時間複雜度是一個會讓大家瑟瑟發抖的主體，在這邊我會用引導的方式讓大家去了解時間複雜度的概念，也希望大家讀完這篇文章後，往後在遇到時間複雜度的時候不會那麼陌生及害怕，甚至還能輕鬆的姿態迎刃而解呦。

怎麼去評斷一個程式(函式)好還是不好 ?

當我們今天程式寫完後，我們不禁會有這樣的疑問，我這個Function的執行效率好還是不好 ？ 最簡單的方式就是，看看這個Function 執行的時間快不快，對吧。但是這樣會產生一個問題，如果當今天有兩台電腦，一台配備是很強的則另一台配備是很弱的，那麼把執行時間當作是一個指標就不是那麼公平了。那有沒有更好的指標呢 ？

答案是有的，如果我們把 Function 的執行「步驟」當成是一個指標呢？第一個Function要執行10萬步才能得到答案，第二個Function只要執行1步，那麼第2個 Function 肯定是比較好的！

我們科學人就是要有實事求是永不放棄連步驟都給你算出來的這種精神。但是~會不會有一種可能是我的步驟跟 input 資料有關係呢？這句話意思是，會不會有某種算法對於某種 Input 資料在處理時特別好，然後對於別種資料會處理得特別差。

這邊我舉一個例子，假設我的Function 是要在長度為10萬的Array裡找到10萬這個數字
我的A演算法從頭開始找到尾巴，B演算法從尾巴往頭開始找，那如果我的10萬這個數字剛好是在最後一個Index，那是不是B演算法在一開始就能被找到，而A演算法則是要在第10萬次才能被找的到 。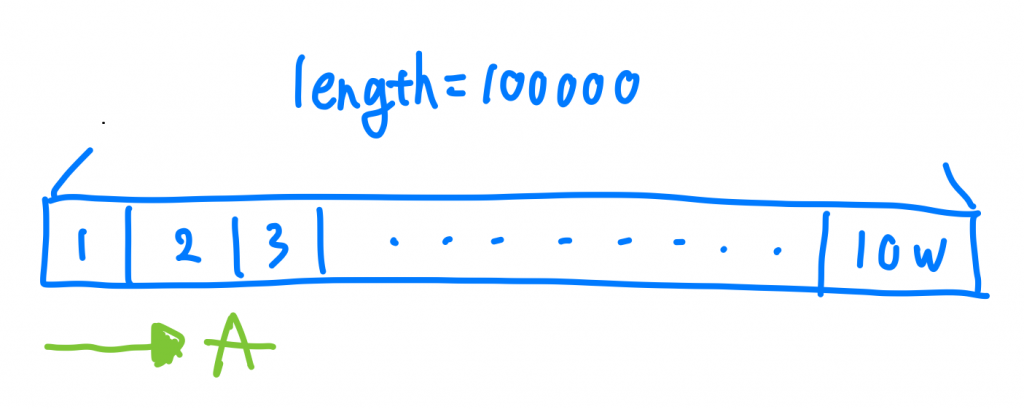


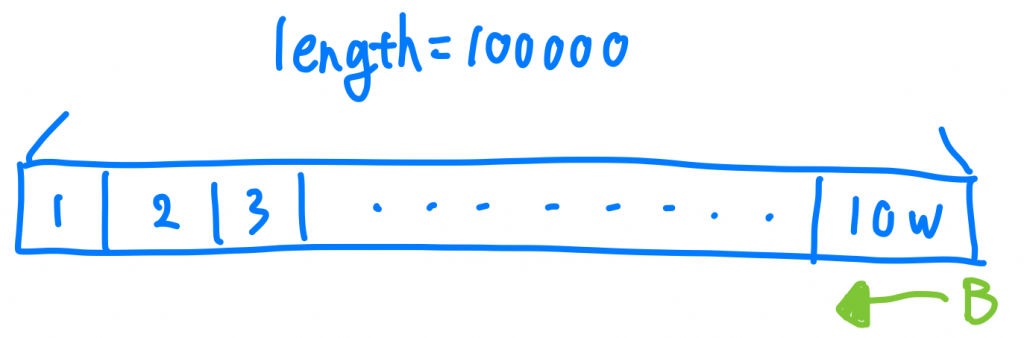
所以就產生了特定的Input會對特別的演算法有偏好，那也不是特別公平的計算方式。那那那那要怎麼辦呢~~不然我們都去評估「最差的情況要執行幾步」，那是不是就公平多了！ 以剛才的範例來說，從頭開始找到尾巴的A演算法他最差的情況就是10萬這個值在尾巴，尾巴往頭開始找的B演算法最差的情況就是10萬這個值在頭，這樣比對就不會有input偏好某種演算法的問題啦，好了，恭喜你學完大家最害怕的Big O。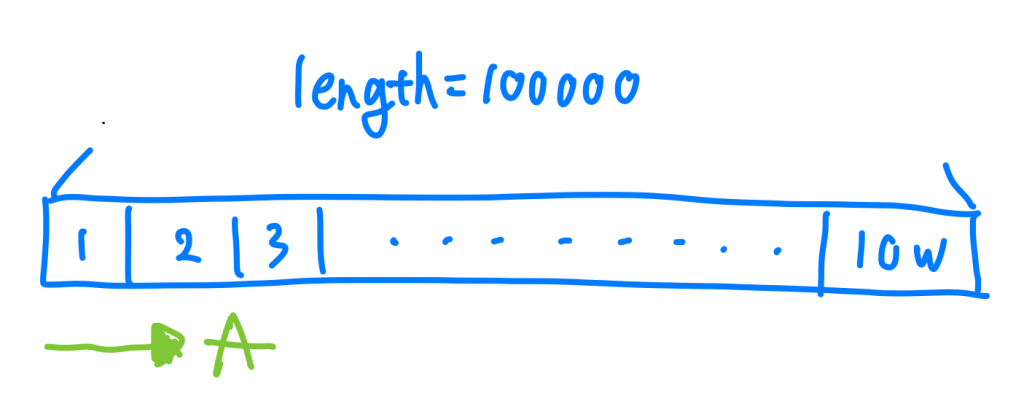


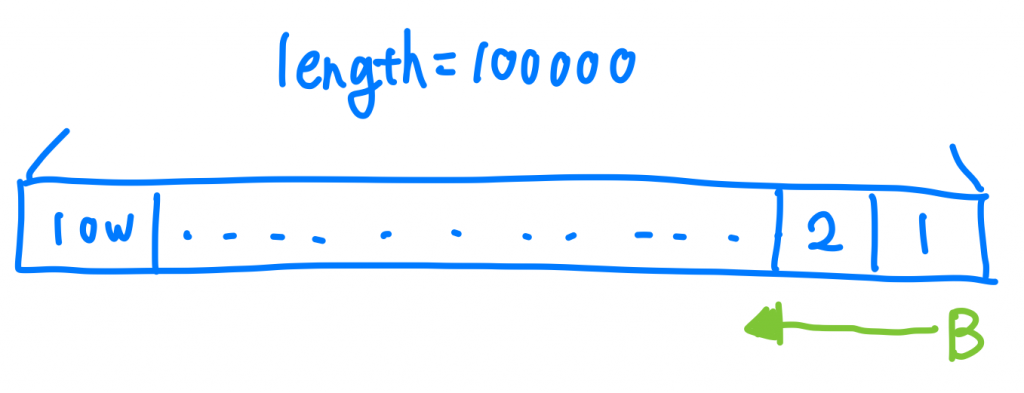
Big O 所討論的就是我們所說的「Worse Case」，中文就是「最差的情況」，這個演算法在最差的情況下需要執行多少次，就是我們時間複雜度在計算的東西。

計算步驟

接下來大家請秉持著剛剛說到「 最差的情況」，讓我們來看看要怎麼計算實際的步驟，其實真的沒有大家想的這麼複雜，我們看看以下的例子。

a = a+1 對於這樣的指令，我們就稱作這是一個步驟

def add_one(n):
      a = a + 1
      return a

以這個add_one()為例，不管我input是甚麼有多大或多小，我都是只做了一個步驟(如果我們把Return加進去算這樣就是2個步驟)，這就是O(1)。

我們再來看第二個例子

def add_n_times(n):
	for i in range(n):
		a += 1
	return a

這個Function在做的是，給一個n那我就把a 加1加到n次。我們來看看這個例子，a+=1跟剛剛一樣算是一個步驟，但是這個步驟我做了幾次呢 ? 答案是n次對吧，如果今天n=5那我就是計算5次，n=100我就是計算100次，所以我們總共是做了n次，這種時間複雜度，我們稱為O(n)。

在看更複雜一點的例子好了，今天如果程式是這樣呢？

def add_n_mul_n_time(n):
	for I in range(n):
	    for j in range(n):
 	        a+=1
	return a

我的a+=1是不是跑了 n * n次呢，所以假如我的n是10，那我總共做了100次步驟，如果n是20那我則是做了400次步驟，這種時間複雜度我們稱之為O(n^2)。

我的函數哪有a+=1那麼簡單

沒錯！當我們真正在寫程式的時候，我們的Function才沒有一個指令就搞定的，那我應該怎麼計算呢 ？
在這邊我要導入一個新觀念給大家，我們不用那麼侷限在到底我的演算法做了多少個「步驟」，當然我覺得有想要去講究到底有幾步那一定是件好事，但是相對來講就太麻煩了，於是乎我們其實應該要更在乎的是我的算法在input持續變大的時候，我要做的步驟數會成為什麼樣的「成長曲線」呢？

我們來看看以下例子，我先以O(1)的例子開始說起。
回到剛剛的add_one(n) 我們可以發現，今天不管我的n多大，我要做的次數永遠都不會變，以這個例子就是只執行一個步驟。

那如果今天我的程式變成這樣呢

def add_one(n):
    a+=1
    b+=2
    c+=3
return a, b, c

是不是依然不管我的n有多大，我始終都做3次而已。如果我們把輸入大小跟步驟數當成X, Y軸我們會發現他就是一條直直的水平線。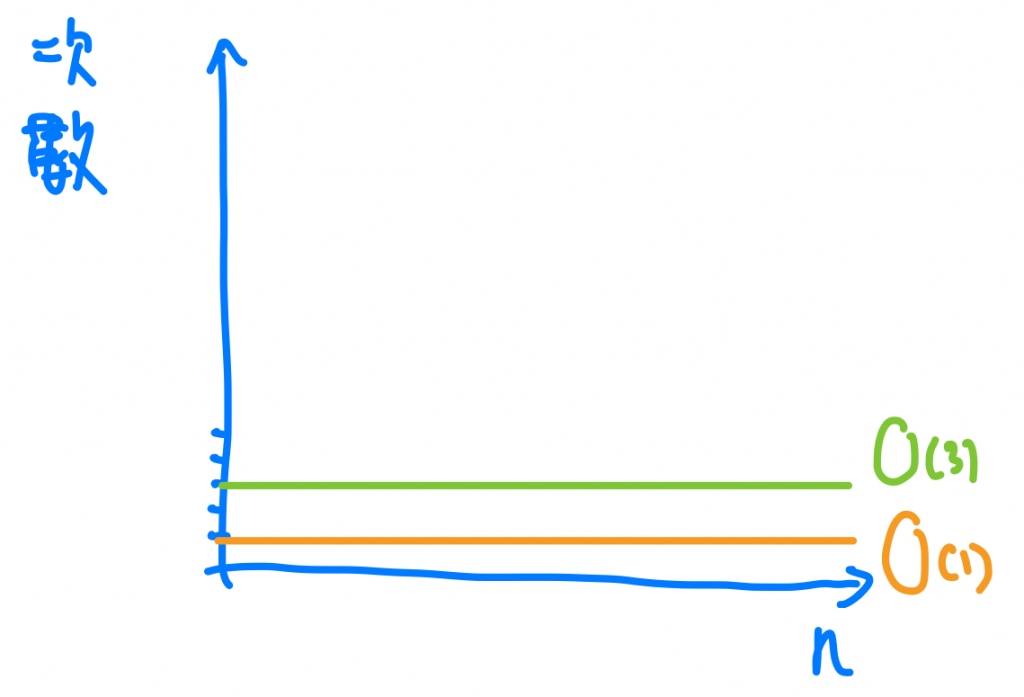

我們在來看看另一個O(n)的例子，一樣我們把它改成

def add_n_times(n):
	for i in range(n):
		a+=1
        b+=2
        c+=3
	return a, b, c

我們總共做了幾個步驟呢 ? 3*n個步驟對吧~那我們一樣把它畫在X, Y 軸上，我們會發現他是一個斜斜的直線，也就是線性的直線。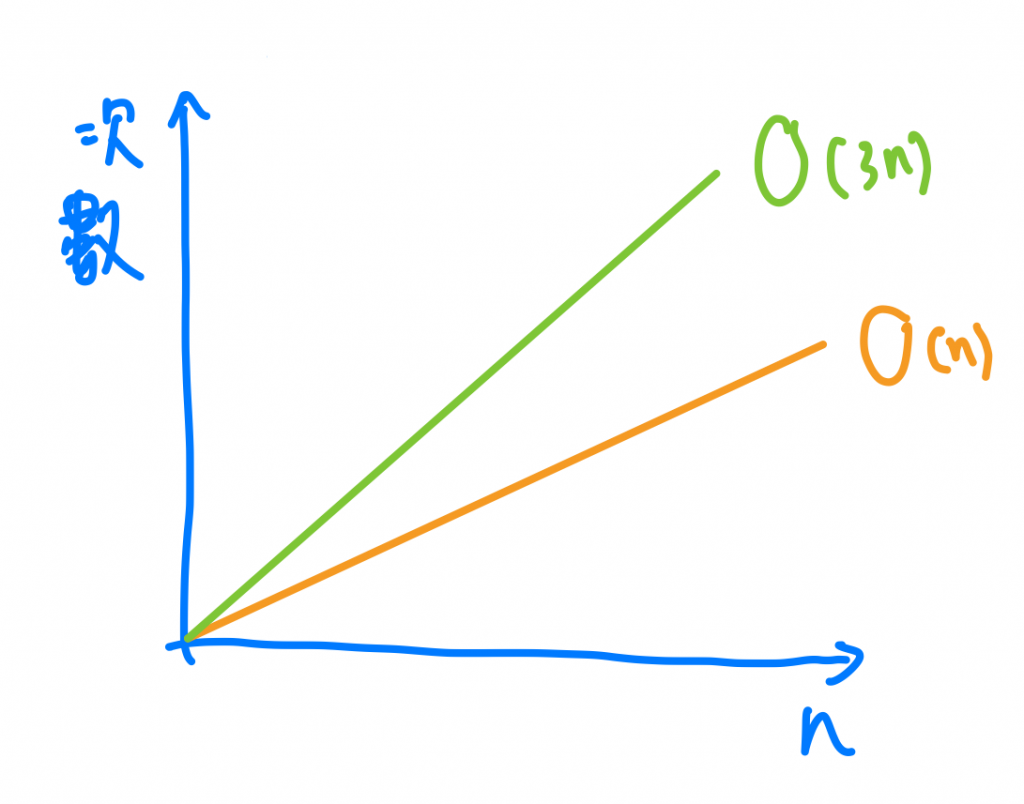

最後我們來看看O(n^2)的例子，我在偷偷修改一下

def add_n_mul_n_time(n):
	for i in range(n):
	    for j in range(n):
 	        a+=1
	        b+=2
            c+=3
	return a, b, c

到這邊大家應該也覺得不難了吧，我們總共做了3*n^2次，我在把它畫到X, Y 軸上，明顯他就是一個曲線了。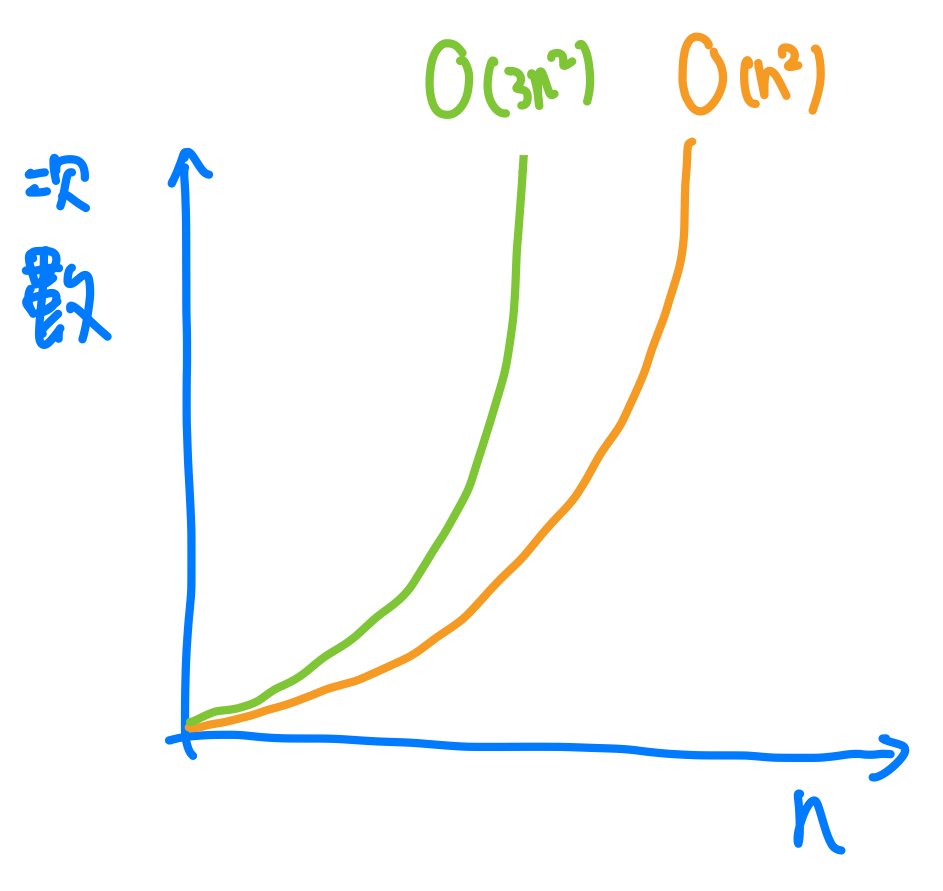

看完以上例子，我們在回頭看我剛剛說的「成長曲線」，就不難發現，以我們剛才舉例的例子來說，執行了n次跟3次的步驟他始終是一條「平行線」，執行了n跟3n步驟的他始終是「斜線」，最後執行了n^2跟3n^2的步驟他始終是「曲線」，這就是我們所謂的成長曲線。

Big O 算法

我們把剛剛的想法統整一下。

1. 找到Worse case
2. 計算確切的步驟數
3. 要知道他是哪個成長曲線

步驟1我想大家都沒問題，接下來我們來看看要怎麼從步驟2到步驟3，其實答案非常的簡單，把步驟2公式化後，取最大的次方項在去掉常數就可以了。我來舉個例子，假如今天步驟2我們算出來是4n^2 + 5n+1那我們就歸類成是n^2的成長曲線級別。在這邊我相信大家會有一個疑問是，那5n呢為什麼不用理他，我們可以來看看當n很大很大的時候，這5n對整體的步驟數影響其實並不是很大(例如：當n=100時，那4n^2是40000，5n則是500)，所以我們會忽略它。

成長曲線是我自己認為比較好理解的說法，實際上大家都還是會直接說「Big O n」, 「Big O n」平方等等這種說法。
另外再補充一點是我們會稱 O(1)為常數時間，O(n)為線性時間，O(n^2)為次方時間。
另外有O(log n)這種時間複雜度，我會等到後面章節再跟大家說明會比較清楚喔。

總結

今天篇幅很長，我們從怎麼去比較一個Function好與壞到計算步驟，接著我們了解到什麼是成長曲線，最後扎扎實實的了解了Big O，希望今天這篇文章在往後對各位職場生涯上能有很大的幫助喔。