今天我們來看看DFS跟BFS的題目吧！

BFS跟DFS的題目有幾件事情要注意一下，這也是我做題下來發現的小技巧。

• 很多時候DFS跟BFS都是可以解決問題的。
• 之前我們再介紹圖的時候都是用相鄰矩陣或相鄰陣列，但是有時候圖也可以用2d array來表示。
• 有時候一些決策的問題也可以用圖來表示，我決策後的狀態改變就是我的節點，我的「決策」就是我的邊。
• DFS通常會用在「有沒有」路徑，BFS通常會用在找「最短」路徑。

範例1-Binary Tree Right Side View

我們先來看看第一題。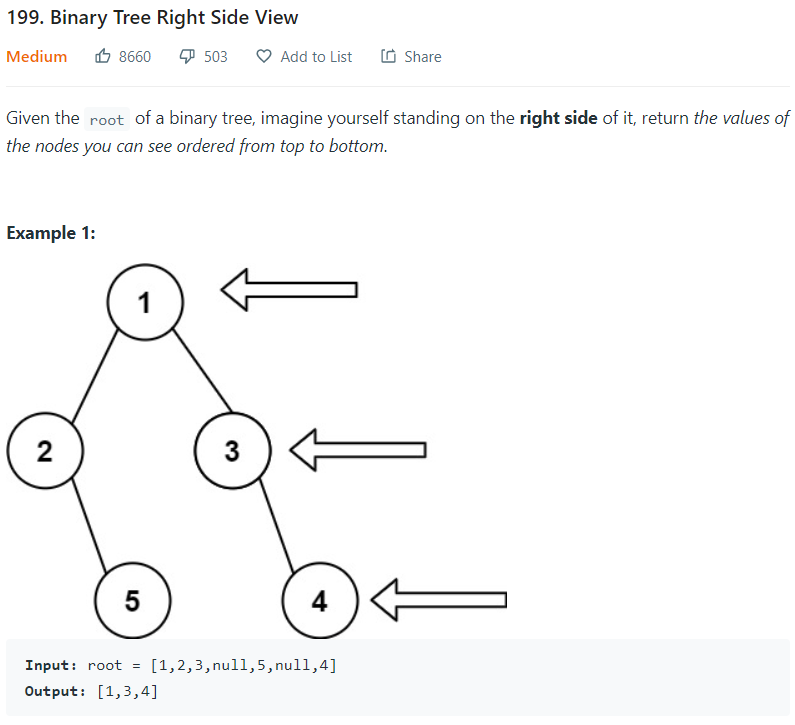

一開始看到的時候會覺得是不是一邊往右邊走然後一邊把節點的值記錄進res就好了。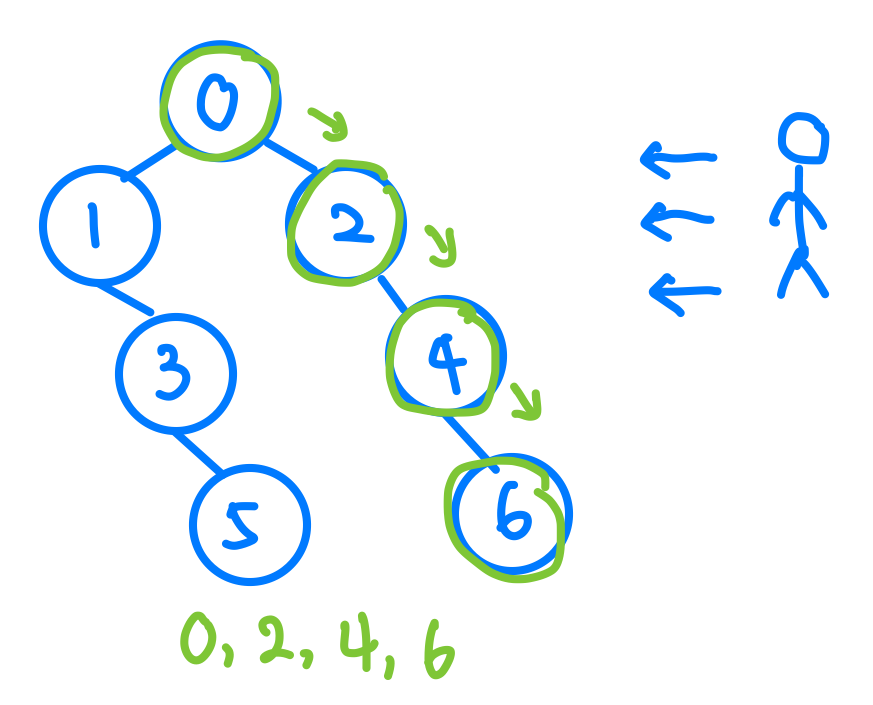

然而我們會發現，如果是這種情況的話就會有錯誤了，因為節點「5」是沒有任何節點擋住它的，所以它也應該要能被看見。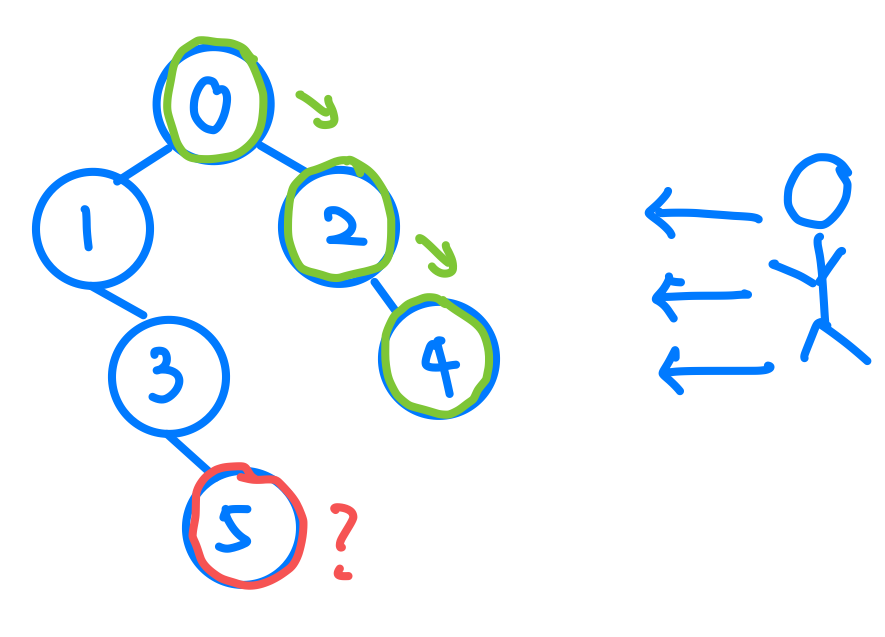

我們來想想看我們要做甚麼呢？其實我們是要找每一「層」最右邊的節點對吧！關鍵字「層」出現了，所以我們就可以使用BFS來做會變的非常簡單。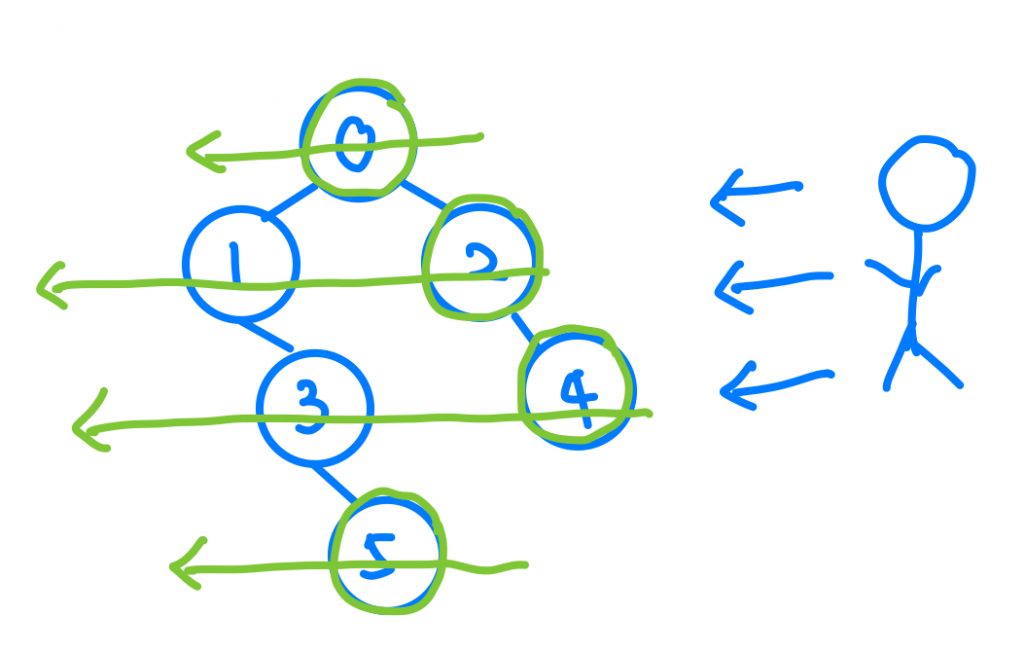

我們的思路是這樣，我們用BFS來尋訪這棵樹，依序把左節點跟右節點加入Queue，接著把我每一層的最後一個節點加入result，這樣就完成拉(當然也可以先加右節點再加左節點，然後把每層的「第一」個節點加入Result)！

這邊因為我們要尋訪完所有的節點，所以時間複雜度是O(n)，空間複雜度的話因為我們是使用Queue所以最多會儲存最底下那一層所有的節點，之前我們也討論過樹最底下那層節點數會是總節點數的一半，所以空間複雜度是O(1/2n)，也就是O(n)。

class Solution:
    def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
        
        res = []
        queue = deque()
        
        if root:
            queue.append(root)
        
        while queue:
            for i in range(len(queue)-1,-1,-1):
                node = queue.popleft()
                if i == 0:
                    res.append(node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        return res
                

範例2-Number of Islands

接下來我們再來看第二個題目，這道題目有兩個特別的地方。
第一，他的圖是用2-d Array來表示的，第二，其實不管是DFS或是BFS都可以解這題喔。

我們可以用最簡單的方式去想，我要怎麼知道這邊有多少個島嶼呢？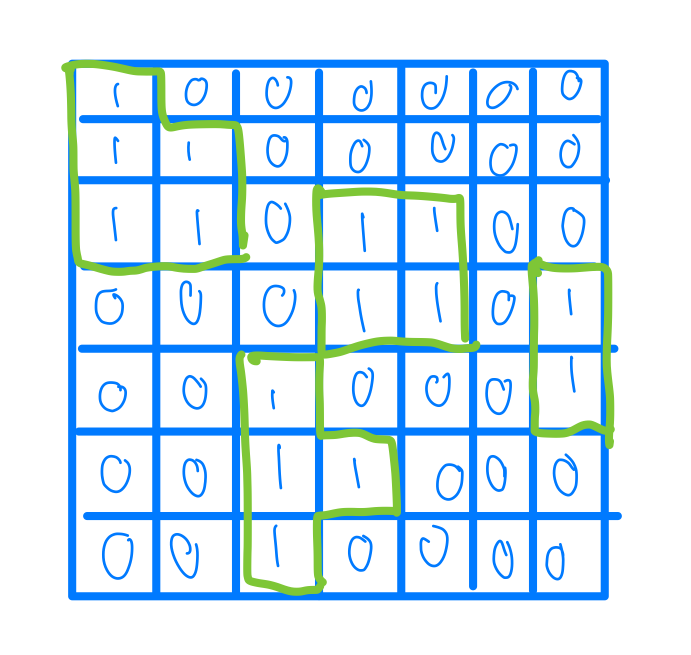

首先我會從頭開始找，一直到找到是陸地的格子，然後看看跟他相連的格子有哪一些，那些相連的格子都算在同一個島嶼上。有了這個思想之後我們可以大概的有一個想法，我們重頭開始遍歷格子，當我們發現這格子是代表陸地的時候，我們就做一個dfs或是bfs把相鄰的陸地也走過一遍，走完一次dfs或bfs我們島嶼數量就+1，但是這邊要注意，為了避免重複算到島嶼的格子，我們可以用一個visit set 來去紀錄我們走過了沒。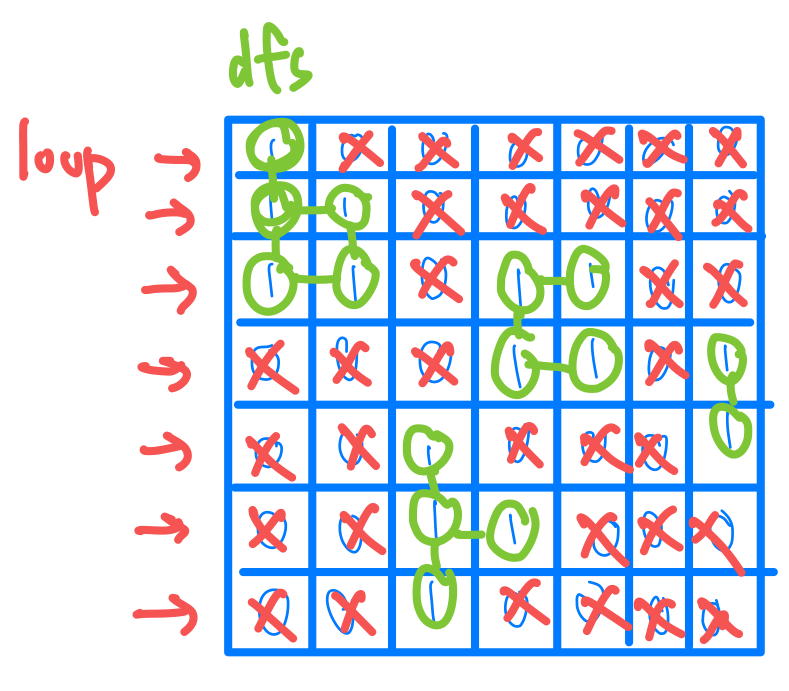

這邊我就選擇用dfs來實作，大家還記得dfs我們可以選擇利用遞迴來實作。
我們dfs的Base Case有幾個

• 已經走過的
• 邊界超出2d array的
• 不是陸地的

另外大家可以看到dfs(r+-1,c+-1)，就代表著我從這個格子要往上下左右4個方向去探索的意思，這個在2d array的dfs尋訪很常見，大家可以記起來呦。

這邊我們也是尋訪完所有的節點，而且如果尋訪過不會尋訪第二遍(有存在set裡面)，所以時間複雜度是O(n)，空間複雜度的話我們有利用到set去存走過的節點，最多也是需要n的空間去存，所以空間複雜度是O(n)。

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        
        rows, cols = len(grid), len(grid[0])
        visited = set()
        count = 0
        
        def dfs(r, c):    
            if( (r,c) in visited or
                r < 0 or c < 0 or
                r > rows-1 or c > cols-1 or
                grid[r][c] == "0"):
                return
            else:
                visited.add((r,c))
                dfs(r+1,c)
                dfs(r-1,c)
                dfs(r,c+1)
                dfs(r,c-1)
        
        for r in range(rows):
            for c in range(cols):
                if grid[r][c] == "1" and not (r,c) in visited:
                    dfs(r, c)
                    count += 1
                else:
                    continue
        return count

範例3-Open the Lock

接著我們來看看這種不明顯是圖的問題的題目。

我們來想想看要怎麼一步一步思考這個問題。首先，我們都會從0000開始，我的每一動都可以選擇讓4個位置的數值+1或-1，所以從0000開始一步我會有8個可能。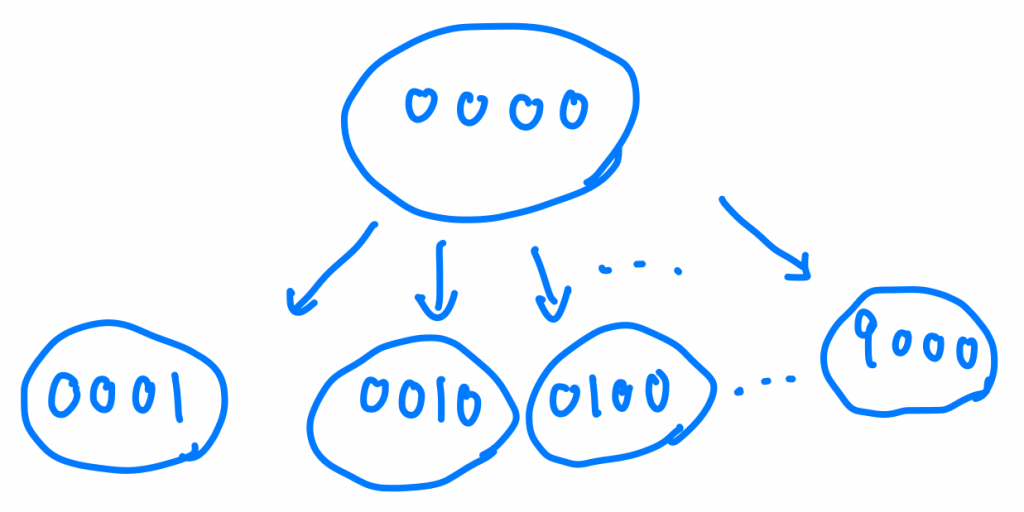

而這8個可能裡面的任何一種，也都可以再有8種可能，我第n「層」就代表著我走了第n步，我們要在最小的「層」找到我們要的答案。
我們把每一個+1或-1的決策當成邊，而決策完後的狀態當成節點。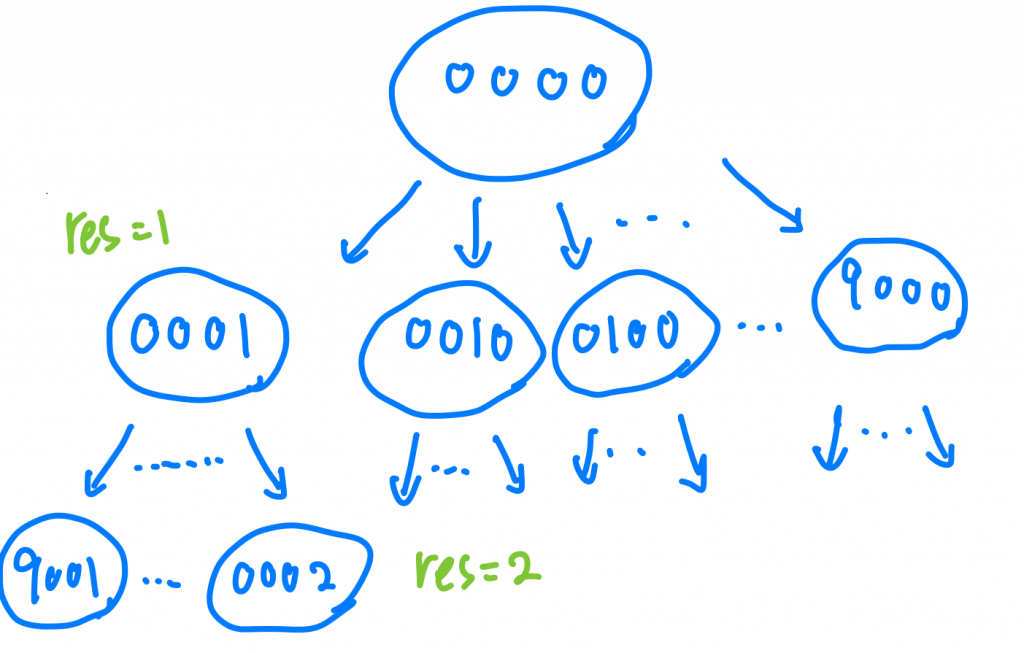

關鍵字「層」還有「最短路徑」出現，我們可以使用BFS來實作，這樣就可以找到到達終點最少的步數。另外如果遇到deadends就直接continue掉，因為我們不會從deadends的狀態再往下走喔。

這邊我們會發現所有的可能其實也就10000種，我全部試完一定會得到答案，所以我的時間複雜度是O(10000)，空間複雜度我們是使用Queue，然後最後一層的節點數最多是5000個，所以空間複雜度會是O(5000)。
所以其實可以說，這一題時間跟空間都是O(1)，雖然有點怪哈哈哈。

class Solution:
    def openLock(self, deadends: List[str], target: str) -> int:
        
        queue = deque()
        visited = set()
        deadends = set(deadends)
        
        def change_digit(digit): # return +/- digit
            if digit == "0":
                return "1", "9"
            elif digit == "9":
                return "0", "8"
            else:
                return str(int(digit)+1), str(int(digit)-1)

        def bfs():
            queue.append("0000")
            res = 0
            while queue: 
                for _ in range(len(queue)):
                    cur = queue.popleft()
                    if cur in deadends or cur in visited: continue
                    if target == cur: return res
                    
                    visited.add(cur)
                    
                    digit_1 = cur[0] 
                    digit_2 = cur[1]
                    digit_3 = cur[2]
                    digit_4 = cur[3]
                    
                    digit_1_upper, digit_1_bottom = change_digit(digit_1)
                    digit_2_upper, digit_2_bottom = change_digit(digit_2)
                    digit_3_upper, digit_3_bottom = change_digit(digit_3)
                    digit_4_upper, digit_4_bottom = change_digit(digit_4)
                    
                    queue.append(digit_1_upper+digit_2+digit_3+digit_4)
                    queue.append(digit_1+digit_2_upper+digit_3+digit_4)
                    queue.append(digit_1+digit_2+digit_3_upper+digit_4)
                    queue.append(digit_1+digit_2+digit_3+digit_4_upper)
                    queue.append(digit_1_bottom+digit_2+digit_3+digit_4)
                    queue.append(digit_1+digit_2_bottom+digit_3+digit_4)
                    queue.append(digit_1+digit_2+digit_3_bottom+digit_4)
                    queue.append(digit_1+digit_2+digit_3+digit_4_bottom)                 

                res+=1
            return -1
        return bfs()