影像濾波(Image Filtering) 技術是對輸入的數位影像進行運算，產生輸出的數位影像。影像濾波技術源自於數位訊號處理(Digital Signal Processing)，包含 濾波器(Filter) 的設計。在數位訊號處理領域中，濾波器也常被稱為核(Kernel)、卷積矩陣(Convolution Matrix)或遮罩(Mask)。

而影像濾波的技術依照數學運算方式可分成兩種:

• 線性濾波 : 數學運算方式為線性(Linear)，也就是輸入影像的像素強度值與濾波器的係數是採用線性組合的方式進行，藉以產生輸出的像素強度值。例如卷積就是典型的線性濾波器，同時也是影像濾波的核心技術。

• 非線性濾波 : 數學運算方式為非線性(Nonlinear)，例如:排序等，或在計算輸出影像的像素值時，採用的運算方式是根據局部的影像資料而定，具有適應性，稱為非線性濾波。

卷積介紹

進入影像濾波實際操作前，讓我們先簡單了解基礎數學理論，也就是影像濾波的核心技術:卷積(Convolution)

「針對兩個時間函數x(t)與h(t)進行數學運算，產生另一個時間函數y(t)的過程，稱為卷積。」

卷積的數學定義如下:

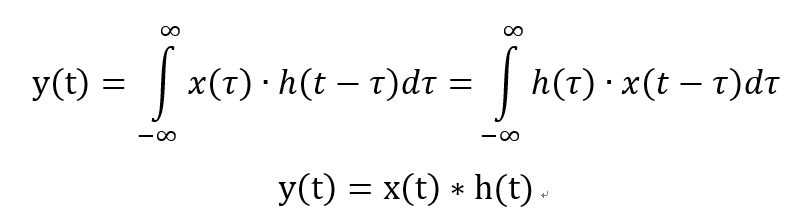
其中，星號 * 為卷積的常用符號。

看到恐怖的積分符號，對我來說就很難受，幸好DSP技術是以數位訊號為主，因此主要是處理在離散時間軸上，因此我們可以換成數位訊號版本的卷積:

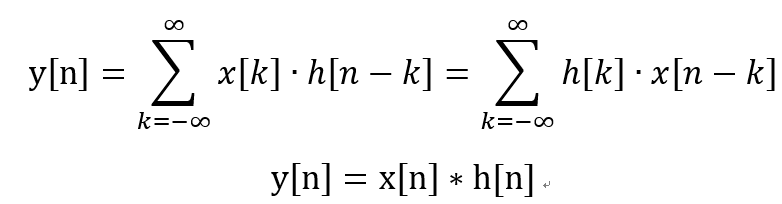
這樣看起來比較舒服一點了。
在數位訊號領域中，h(t)稱為脈衝響應(Impulse Response)，是DSP領域的專業用語。也常被稱為濾波器。

以下讓我們來示範移下簡單的卷積運算:

若輸入的數位訊號為: x = {1,2,4,3,2,1,1}, n = 0,1,...,6
脈衝響應濾波器為: h = {1,2,3,1,1}, n = 0,1,2,3,4

首先，輸入訊號x[n]共有7個樣本(N=7)，而脈衝響應h[n]有5個樣本(M=5)，則卷積y[n]的結果要有M+N-1 = 11個樣本
因此在進行卷積運算前，先在輸入訊號x[n]的兩邊補上M-1=4個0，稱為Zero-Padding，結果如下:

接著將h[t]旋轉180度，也就是左右對調，這也是卷積這個名稱的由來，並將h[0]和x[0]對齊，如下圖:

接著開始進行「積」的運算，也就是把對齊的樣本上下兩兩相乘再相加，得到的結果為y[0]，因此:
y[0] = 0 * 1 + 0 * 1 + 0 * 3 + 0 * 2 + 1 * 1 = 1

然後把h[t]向右移一個單位:

再將對齊的樣本兩兩相乘再相加，得:
y[1] = 0 * 1 + 0 * 1 + 0 * 3 + 1 * 2 + 2 * 1 = 4

繼續向右移到終點為止。以上就是整個卷積的流程，運算看似複雜，實際上Python就有提供一個簡單的函式幫我們計算。

import numpy as np

x = np.array([1, 2, 4, 3, 2, 1, 1])
h = np.array([1, 2, 3, 1, 1])

y = np.convolve(x,h,'full')

print("Convolution y = ", y)

程式碼中的convolve函式即可運算整個卷積結果，雖然卷積的實驗方式非常簡單，但其實背後的數學原理是很有趣的，在許多電腦科學領域中，卷積扮演著非常重要的腳色，理解卷積的原理與方法對於未來學習其他領域的知識是很有幫助的。

另外，在數位影像處理中，影像濾波就是利用二維訊號的卷積，原理其實和一維卷積相同，因此以下就不再贅述詳細過過程，僅列出定義函式以及程式碼供讀者閱讀。

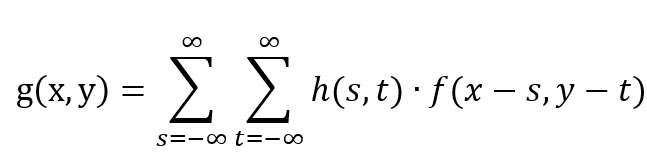
齊中f(x,y)維輸入影像的強度或灰階，g(x,y)為輸出影像的強度，h為濾波器。由於影像濾波在進行卷積運算時，通常牽涉鄰近像素的強度或灰階度，因此常被稱為局部處理(Local Processing)

程式碼如下:

import numpy as np
from scipy.signal import convolve2d
x = np.array([[1,1,1],[1,1,1],[1,1,1]])
h = np.array([[1,2,3],[4,5,6],[7,8,9]])

y = convolve2d(x,h,'same')

print("Convolution y = ")
print(y)

上述程式碼中的same參數，主要使輸入與輸出的數位訊號，總樣本數維持不變，並擷取卷積運算中的部分結果。

那麼今天的卷積介紹就到這裡，有興趣的讀者可至我的Github參考程式碼，謝謝大家!