再往下介紹其他資料結構前，今天我想先來跟大家介紹一個很強大的演算法，Binary Search也叫做「二分搜尋法」，也因為在時間複雜度的章節，我怕大家剛接觸時間複雜度的概念，會比較難聽懂log n這種概念，經過幾天的文章內容希望大家開始對時間複雜度能有比較多的感覺，那就讓我來講講二分搜尋法吧。

Linear Search in Array

想像一下我們今天要在Array中找到特定的數字，我們會怎麼做？這個也太簡單了吧，從頭找到尾就好啦！以這種Worse Case 搜尋法就是要把整個Array找完，時間複雜度就是O(n)囉。

那我們有沒有辦法讓他更快一點？說實話，在雜亂無章的資料裡，我想應該是沒辦法的。甚麼是雜亂無章的資料，也就是這個資料沒有任何的規則、沒有順序，這種情況我們就真的只能從頭開始一筆一筆尋找了。

在有排序過的資料中尋找

現在我們想想看字典、電話簿這類的東西，如果今天我要找一個英文單字，我們會從第一頁開始找嗎？鐵定是不會的吧，假如我要找的英文單字是 f 開頭，我翻到中間後看到是m開頭的單字，那我只需要往前找，後面我根本就不會考慮，對吧？然後我往前隨便翻發現在是e開頭那我敢肯定我的單字一定在e這頁跟m那頁之間，於是我們重複以上步驟，最後順利找到我要的單字。
如果你曾經這樣做過，恭喜你，你已經會二分搜尋法的精神了。

我們來思考看看，為什麼我們可以用這樣的方式來找到我要的單字？其實最大的原因就是，資料是有順序性的，b排在a後面，c排在b後面，所以當我一翻開我可以知道我要找的單字是在我現在的前面還是後面。

Binary Search

帶著剛剛字典找單字的想法，我們來看看如果我的資料是有「排序」過的，我是不是能用一樣的邏輯去找到我要的資料呢？
我們來看下面這個例子，假設我們的Array是這樣[2, 4, 6, 9, 15, 18, 20, 54, 98, 101, 105]
我們想要尋找9這個數字，我可以怎麼找呢？我們先定義一個左邊的pointer跟右邊的pointer，這兩個pointer所包含的範圍就是我的資料可能存在的範圍，所以一開始我的left pointer = 0指向第一個數字，right pointer=len(arr)-1指向最後一個數字。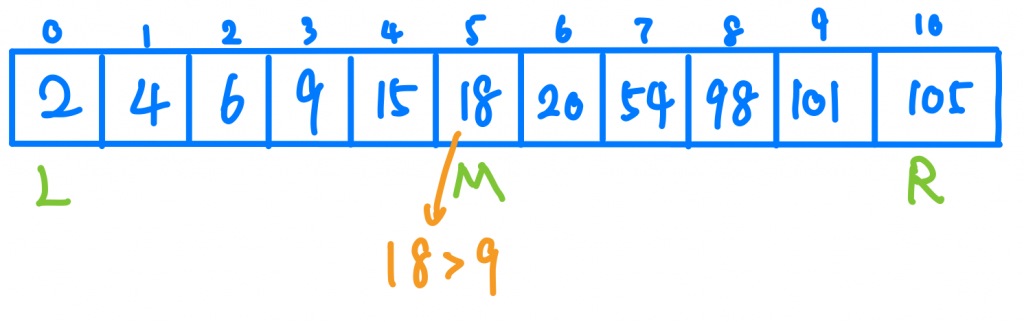

現在我們要開始從中間找有沒有我要的資料，中間的index就是 (left+right)/2 = 5 值為18，我們發現9比18小，這代表甚麼？因為我們資料有排序過，所以9一定會在18的左邊，我們可以完全不用考慮18右邊的數字，這時候我們更新right pointer。
接下來我們重複以上動作，就能找到9這個數字。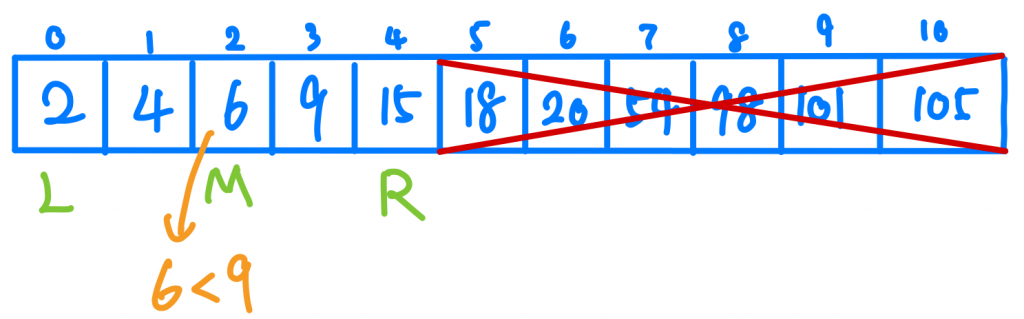

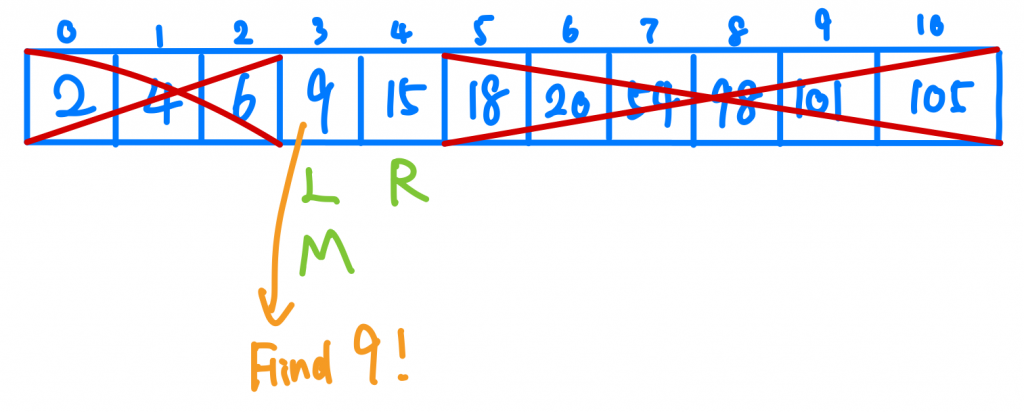
Binary Search的時間複雜度

那麼 Binary Search的時間複雜度是多少呢？每次搜尋後都少一半那就是O(1/2n)。錯！這是剛接觸時間複雜度的人容易犯的錯。如果想計算時間複雜度，那首先我們要來看看Binary Search實際上到底做了甚麼。其實在每一次的搜尋中，我都排除掉一半的可能，用Array可能不好理解，其實我們可以把剛剛的情況轉換成Binary Search Tree。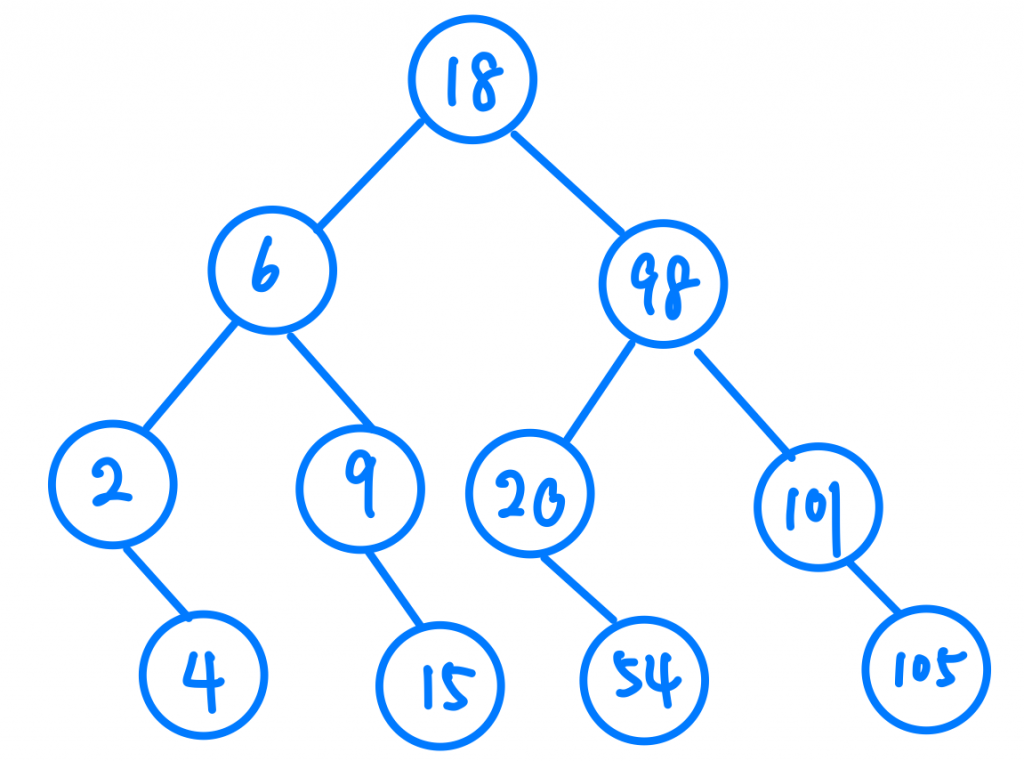

還記的Binary Search Tree的概念嗎？每個節點的右邊都一定比他大，左邊也一定比他小。我們從Root Node開始，發現9比18小，這代表我要往左走，大家可以發現是不是跟Array一樣，我們完全不用考慮Root Node右邊以後的值了，也就代表一個操作後我就排除掉一半的可能了，那再來就很簡單囉，我們最多會走幾步？其實就是樹的高度，也就是log n。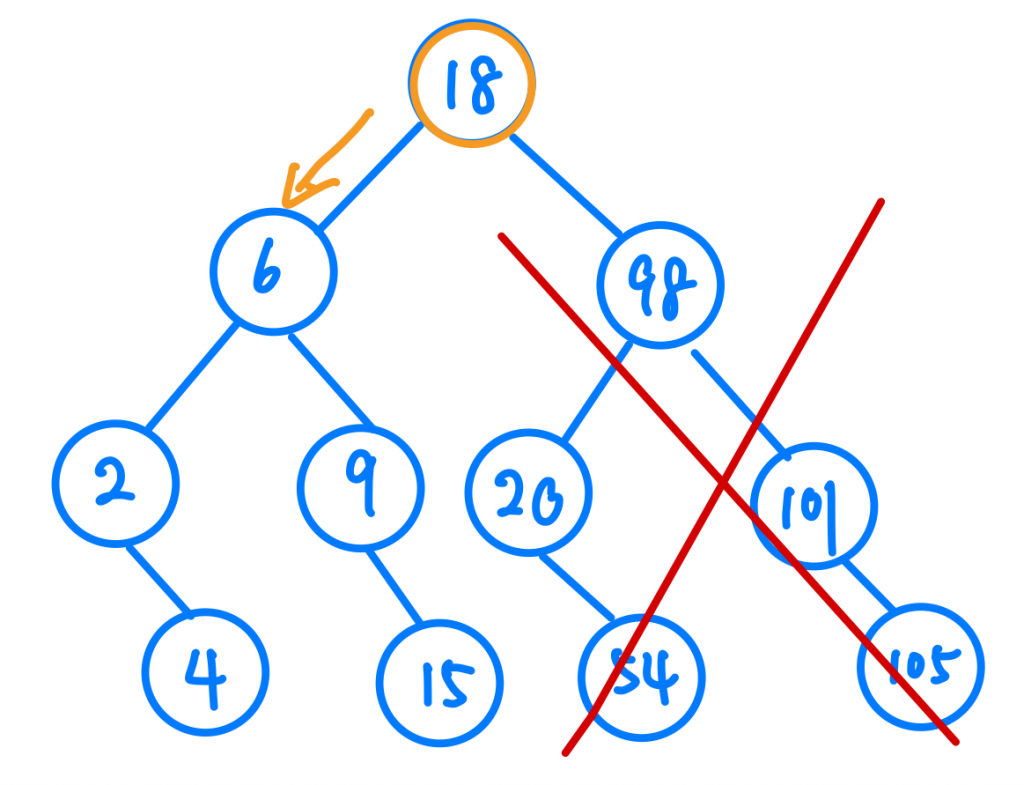

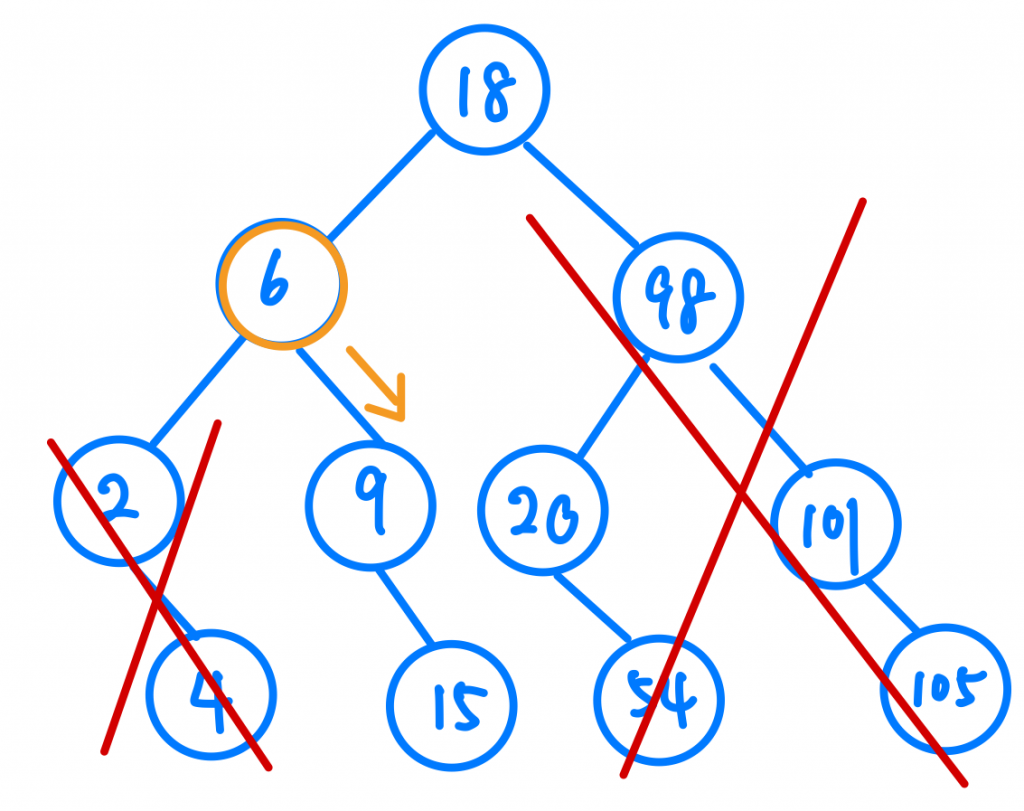
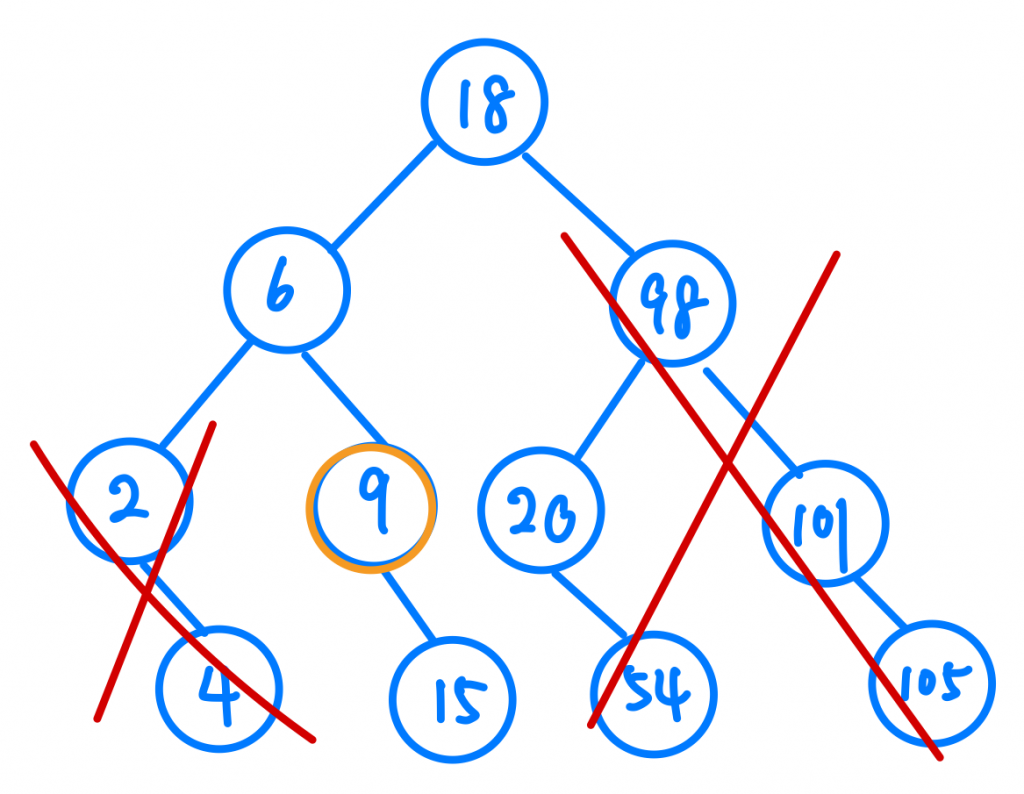
總結

今天的篇幅有點長，我們從一般的線性搜尋演算法到二分搜尋法，再把Array的二分搜尋映射到Binary Search Tree上去驗證他的時間複雜度，如果對於樹還不熟悉的讀者，我建議可以去看看上一篇的內容呦。