樹（Tree） vs. 圖（Graph）

一個資料結構，如果他是沒有「循環」 (Cycle) 在內的，那他可以被拉成「樹」

如果存在「循環」在內，那他就叫「圖」

因此我們可以稱「樹是一種圖」

樹

以下的術語，我們會以搭配這張圖來輔助說明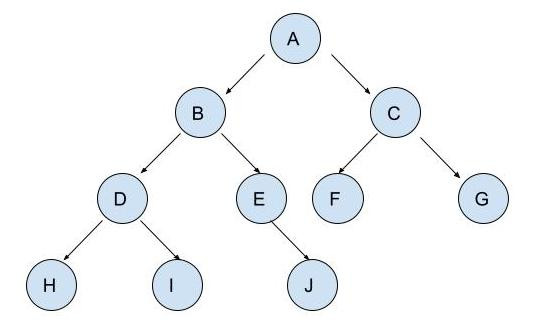

節點家族

假設我是節點 D

1. Parent Node(父節點)

   • D 的父節點為 B

2. Child Node(子節點)

   • D 的子節點為 H, I

3. Sibling Node(兄弟節點)

   • 父節點的所有子節點互為兄弟節點（表兄弟跟堂兄弟都不算）
   • D 的兄弟節點為 E

4. Root Node(根節點)

   • 根節點沒有父節點，因此也沒有任何兄弟節點
   • 一棵樹只有一個根節點
   • 這棵樹的根節點是 A

5. Leaf Node(葉節點) / Terminal Node(終端節點)

   • 葉節點沒有任何子節點
   • 這棵樹的葉節點是 F, G, H, I, J

Terms of Tree

1. Degree（度）：子節點個數
   • 例：Degree(Leaf Node) = 0
2. Level（階層）：以下我們以遞迴來定義
   • Level of Root = 1
   • Level of Child Node = Level of Parent Node + 1
3. Height / Depth (深度):
   • 一棵樹中，最大的階層為這棵樹的深度
4. Width (寬度):
   • 階層 n 的節點數量
   • 例：Width of Level 2 = 4
5. Breadth (廣度):
   • 葉節點的數量
   • 例：Breadth of this tree = 5

Binary Tree vs. Binary Search Tree

二元樹（Binary Tree）：簡稱 BT

二元搜尋樹（Binary Search Tree） ：簡稱 BST

「二元搜尋樹」 是一種 「二元樹」( BST <= BT <= Tree )

所以，二元搜尋樹需要先滿足二元樹的條件！

Binary Tree

簡單來說，每一個節點最多有兩個分岔

Family of Nodes

一個節點的家族關係：

1. Parent Node(父節點)：

   • 在二元樹裡面，一個節點最多有一個父節點
   • 如果一個節點沒有父節點，那他就是樹根(root)

2. Child Node(子節點)：

   • 在二元樹裡面，一個節點最多有二個子節點(兩個分岔)
   • 如果一個節點沒有子節點，那他就是樹葉(leaf)

3. Sibling Node(兄弟節點)：

   • 在二元樹裡面，一個節點最多有一個兄弟節點
     • 父節點有兩個分岔，自己是其中一個
     • 如果父節點有兩個子節點，那另一個節點就是自己的兄弟節點

Complete / Full Binary Tree

Complete Binary Tree

假設一棵樹有 n 個節點，這些節點必須「由左而右」、「由上而下」放置

Which is a Complete Tree?

(A)

(B)

為什麼不是 (A) ?
D 的 右子節點仍是空的，不能先往右放置新節點

Full Binary Tree

• aka. Perfect Binary Tree
• 所有非葉節點都有兩個子節點
• 所有節點都在同一階層
• 高度為 h 的樹有 1 + 2 + 4 + ... + 2^(h-1) 個節點
• Complete Binary Tree >= Full Binary Tree

二元樹的延伸

1. 二元搜尋樹 （Binary Search Tree）
2. 二元堆積 （Binary Heap / Heap Tree）
3. etc.

接下來，我們會把重點放在「二元搜尋樹」上。