前言

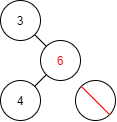
接著我們進入到了二元搜尋樹，以下將會先講解二元搜尋樹的定義、並談及某一些特性，之後會在談及 BST 的各種操作之演算法，由於未來要談及的高等樹 AVL Tree 是 BST 的一種，所以要先將 BST 理解清楚，未來才不會無法理解高等樹！

BST 的定義、特性

先了解到 BST 視為 BT 的一種，因此 Node Degree 必<= 2

1. 左子點必 <= 父點
2. 右子點必 >= 父點
3. 子樹必須都為 BST

由於定義規定了左子點與右子點的大小關係，因此可以發現，若給予一個 List 並依此建立一棵 BST 時，使用不同的數字當作起始點插入，會造成 BST 的長相不同，因此要記得 BST 的長相會受到插入順序而影響

也因為定義的關係，當使用 Inorder Traversal 去遍歷 BST，可以取得 Sorted List

BST Build & Delete

Build

若給予 List [1,2,3,4,5] 建立 BST，會形成 Right skewed BT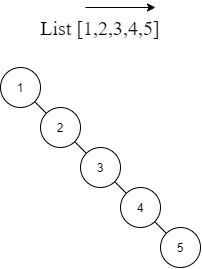

若給予 List [5,4,3,2,1] 建立 BST，會形成 Left skewed BT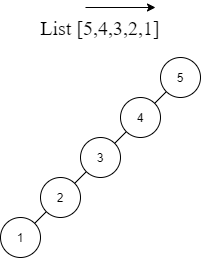

若給予 List [3,2,1,5,4] 建立 BST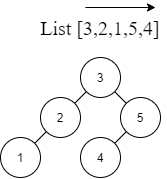

由此可知，雖然 List 中元素皆相同，但依照不同的順序，便會產生不同的 BST

Delete

先針對此BST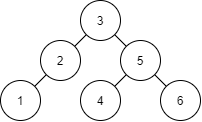

刪除 Degree-1 Node 2：將 2 刪除，並連結父點與其唯一子點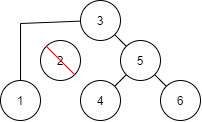

刪除葉節點 1：直接將葉節點刪除即可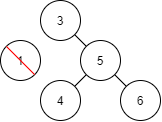

刪除 Degree-2 Node 3：將 3 刪除後，以左子樹之最大 node 或是右子樹之最小 node 取代之，在針對被移走的點進行 Degree-1 or 葉節點的刪除 ( 本次採右子樹最小 node取代之 )