Plan for what it is difficult while it is easy, do what is great while it is small.
> -- Sun Tzu

The scramble

Revisit ruwix, and let's play this scramble!

While grubiks is hardly playable, it can give you a solid 3D sense. Ruwix, on the contrary, while I appreciate it, it really doesn't make any sense until you get very familiar with it. Even if so, it still doesn't feel like the original physical skewb at all, at least for me. Please forgive my rant, dear ruwix!

Stage 0: know what we are doing

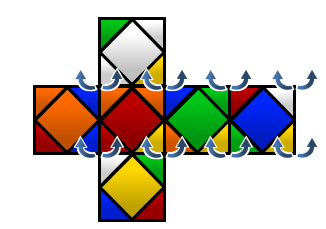
Recall: the cut surface of a skew is a regular hexagon. On the ruwix interface, as shown in the figure, the bold lines stand for the cut on each face, and the red cycle stands for the origin for the rotation,

To visualize the rotation better, the following clip shows the rotations from 8 different conners, and their effect:

Since it is a net representation of the puzzle, it can be bizzare to watch the rotation on edge faces. Anyway, it is harder to reason the puzzle like what we did back in Part II, but still I will try to explain what has been done. Actually, I don't really feel that I make sense out of the interface, so I always have my physical skewb at hand for reference of the rotations.

I want to reuse a similar notation system as what I did in Part II, but a quadrant version to indicate the corner piece. Also, there is no cells here, only faces. I name them as (from top to bottom and from left to right) Y+, X-, Z-, X+, Z+, and Y-. In the following figure,

For example, X-Q2 is red and Y+Q0 is white. Another exmaple, note that X+Q0, Z+Q1 and Y+Q0 belongs to the same corner. For the center piece of each face, I will just call them like Z-O, where O stands for origin.

Also, the given controls L/F/R/B corresponds to the clockwise corner twist of X-O3/Z-O3/X+O3/Z+O3, respectively. The X/Y stands for a clockwise X-/Y-axis-twist to the whole puzzle with respect to X+/Y+.

Stage 1: finish all corners

Anyway, let's solve it.

1-1: finish an adjacent corner for an edge

Our goal is just to fix Z-Q2 and try to complete Z-Q3 in this part.

There is an interesting property of skewb corners: they actually forms two subgroup. Corners in the same subgroup only go to each other's position, but not to those of the other subgroup. Linking all corners in a subgroup forms an embedded regular tetrahedron of the cube.

So basically, there is only two cases for the corner that should be in Z-Q3. It at Z-Q1, or it is not. If it is the former, a counterclockwise twist at Z-Q1 can move it to Z-Q3. If it is the later, it belongs in a 3-cycle generated by the R operation, so we can try just push a few times of R and see if the cube comes to Z-Q3.

We didn't consider orientation yet. If the orientation isn't right, we just twist it away, rotate around the corner piece so that its orintation changes but position is not. This rotation should also be done at a free position, which does not move our Z-Q2. I will just skip the discovery phase, and show the sequence here: R Z+Q1 R'. Just repeat it until it is aligned with Z-Q2. At most twice is enough because it is a 3-cycle as well.

1-2: finish 4 corners for a face

Applying the subgroup property, we can safely repeat Z+Q0 and Z+Q1 until respectively Z-Q0 and Z-Q1 are the correct corner piece. Then let's move on to fix the orientation for them.

For Z-Q1, the sequence is L' R' L Z+Q0. Repeat at most twice and see if the corner comes back with the correct orientation. Note that the final move should be a clockwise twist, or equivalently two counterclockwise twist. For Z-Q0, the sequence is F B F' Z+Q1'.

The second twist is to move the corner away. Roughly speaking, the corner goes through rotations of two different axes, so it comes back with a different orientation.

1-3: finish all corners

Move the completed corners up to Y+ by X. Try F L' F' L sequence a few run and see what happens. If at any moment the Y- contains two correct colors, rotate the whole puzzle with Ys until the colors in the Y- face are all wrong, and keep trying the F L' F' L sequence. The basic idea is that, the sequence is a 3-cycle. If Y rotation is never use, then result of Y- face from this sequence is either perfectly correct for 1 of the cases or all wrong for 2 of the cases, because all corners rotate 120 degrees. If you see there is two correct colors and repeat the sequence, the result of Y- is 2 correct colors at diagonals for 2 of the cases, and one is all wrong. So a symple way to resume the all correct status, is to rotate the whole puzzle around Y axis at the right time.

the progress so far

Please forgive me that I messed things up, so I started with another scramble...

Conclusion

We learn to play with skewb and the ruwix interface today. It is really weird at first, but when you get used to it..., it is still weird. But at some point you just start to forget the weirdness and move on. The skew nature provides a little bit frustration and also a bit of the fun. It is surprising that many people actually like the puzzle so that WCA accept skewb as an official competition event.

Hope you enjoy it. We will solve it tomorrow and close the warm-up with some math properties of skewb.

小結

解了一半的 skewb。