For me, I pride myself on every aspect of the game.
-- Suzuki Ichiro

Stage 2: solve the centers and all done

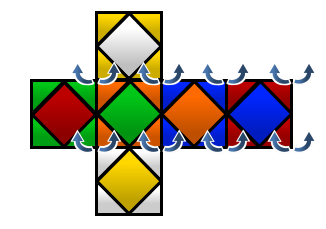
There are different conditions in this case, but in general, I only use one core algorithm: 9 times of (L F') , which is a 2-cycle that exechange two pairs of center piece, X-O and Y-O, and Z-O and X+O. A general rule of thumb is, applying this core algorithm a few times to see if there is any complete face, if not then do X or Y to change the puzzle orientation and try again. Once any face is completed, rotate it to Y+. Once any second face is done, move it to Z+. And then with appropriate setup, the core algorithm should be able to solve the whole skewb.

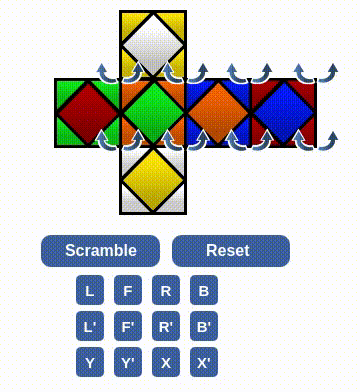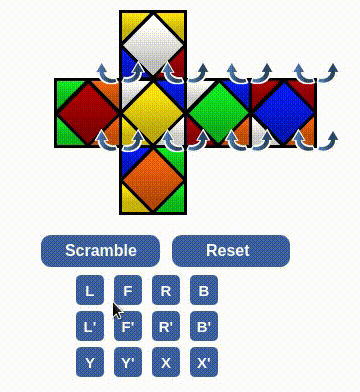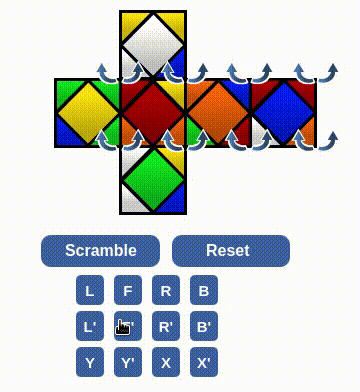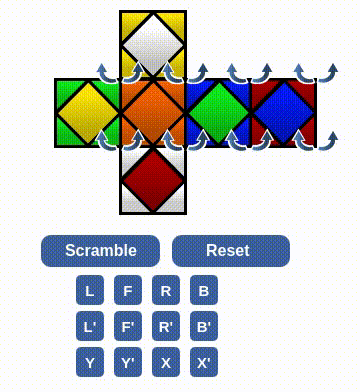
There were some click error, but the recovery process was skipped. The following clip solves a situation that looks like we finish three centers. Maybe there is a algorithm for this 3-cycle center piece, but anyway I don't know it. I will just apply the sequence to do two 2-cycle sequences. The first will ruin one finished face, but the second time it can be completed again with an appropriate setup.

Interesting, the above strategy didn't work. I decide to do a different setup, where I don't want Z+ is a complete face.

Now the rest two pairs look like suitable for our (lame) sequence. Now with a good setup,

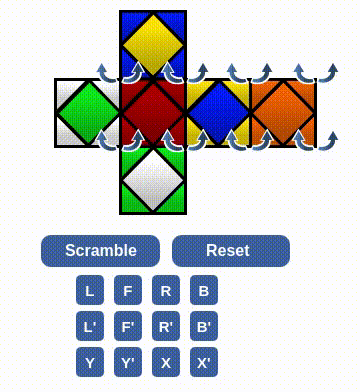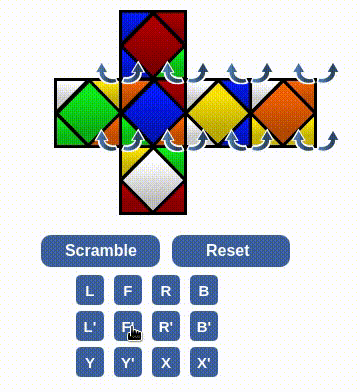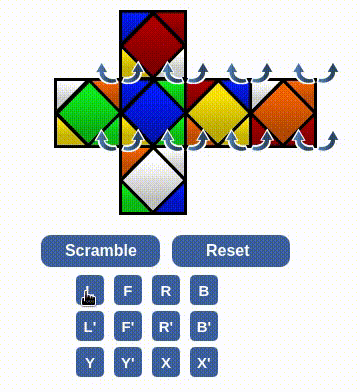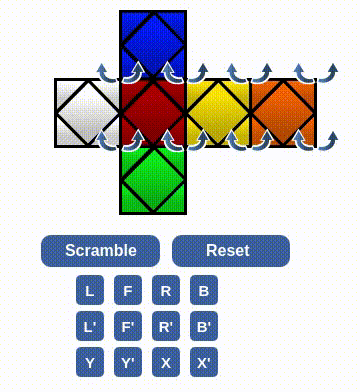
Horray!

Some more math on skewb

In the first day of Part III, I mentioned, a ray from origin to a vertex can serve as a valid rotation axis for a cube, and the cutting surface is a hexagon. We can let the origin be the origin of the coordinate, and make all 6 faces of the cube perpendicular to exactly on of the axes in X, Y, or Z. Also, we let this cube's size be 2 units. Then, for the vertex (1, 1, 1), vector (1, 1, 1) itself is a valid rotation axis and it is perpendicular to the cutting hexagon.

It is interesting that, the boundary of the cutting hexagon can be view as the intersaction between the cutting hyperplane and the cube's boundary. The later is trivial, and we can easily derive the equation of the former from known information:

1. The normal vector of the cutting surface is identical to the vertex coordinate, because the start point of a valid axis can always be the origin.
2. The cut surface, as a hyperplane, contains the origin. No matter how controversial the definition of deep-cut is, skewb is certainly a origin-cut puzzle without doubt.

so basically, we have the hyperplane equation of the 4 rotation surfaces

• x + y + z = 0
• x + y - z = 0 (normal vector (1, 1, -1))
• x - y - z = 0 (normal vector (1, -1, -1))
• x - y + z = 0 (normal vector (1, -1, 1))

The 6 faces of the cube have hyperplane representation as well, they are

• X = -1
• X = 1
• Y = -1
• Y = 1
• Z = -1
• Z = 1

Consider the first x + y + z = 0 for now. The intersection is a 2D area, so of courese there are infinite points within the intersactions. However, I will propose a scheme to choose a interesing set of points instead of random ones in later post with prooves, but now the rule of thumb is the set should be eactly on the boundary of the cube. So for the first quation, the set of points are

• (-1, 0, 1)
• (-1, 1, 0)
• (0, -1, 1)
• (0, 1, -1)
• (1, -1, 0)
• (1, 0, -1)

It is not obvious for a 2D being to feel that these 6 points forms a hexagon in the 3D space. We will have a very similar feeling as they do later when we try to figurre out a 4D skewb. Basically we can claim, Without loss of generality, other three hyperplane equations will have similar attributes. I will leave this general claim in later posts.

Conclusion

We derive a systematic solution and solve the skewb with it. After that, the basic math about a skewb is briefly explored. By doing so, I show the readers that my math toolbox on this matter will mainly be cartesian coordiate and vector. Tomorrow, we will start the advanture with hyperskewb.

小結

解開 skewb 並探討一些它的幾何性質。