今天終於要來講遞迴的部分，其實實際上我們在撰寫遞迴的Code的時候，不會真的那麼在意每一個Call Stack的細節，我們更多的是去定義他每一層狀態的關係，我們更需要注意的是遞迴的「思想」。

遞迴的思想

該去怎麼思考一個遞迴的問題？我想這是一開始接觸遞迴時大家一定常有的疑問。在這邊我要很不負責任的跟大家說，其實我個人認為，更多的是「經驗」，而這個經驗要靠平常用不同面向去思考同一個問題。其實可以用迴圈解決的問題也可以用遞迴來解決，相反的可以用遞迴解決的問題也可以用迴圈來解決。

那甚麼時候該用迴圈，甚麼時候該用遞迴呢？

答案是都可以，取決於你看待這件事情的「角度」。我來舉一個生活化的例子。

假設今天iPhone20上市，大家都搶著要去排隊購買，於是我們一到現場才發現，挖~竟然前面大排長龍，然後這時候，店家的號碼牌機器壞掉了，所以我們也不知道自己前面到底排了多少人自己是排第幾號？這時候我們要怎麼計算呢？

• 方法一 : 第一個方法就是，我就移動到列隊的旁邊開始從第一個人開始數，數到我時我就知道我是的幾個人。
  有沒有其他比較懶惰的方法呢？其實是有的，我們接著看下去。
  
• 方法二: 我去問我正前方那個人說，ㄟ~請問你是第幾號，那我把他的數字在加1我就知道我是幾號啦。
  

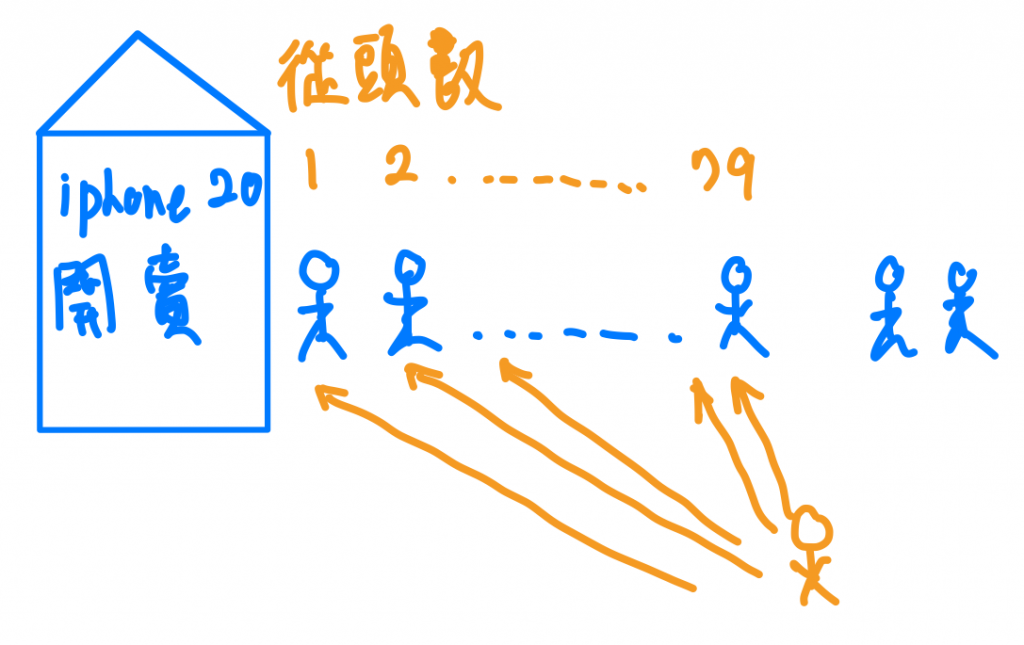
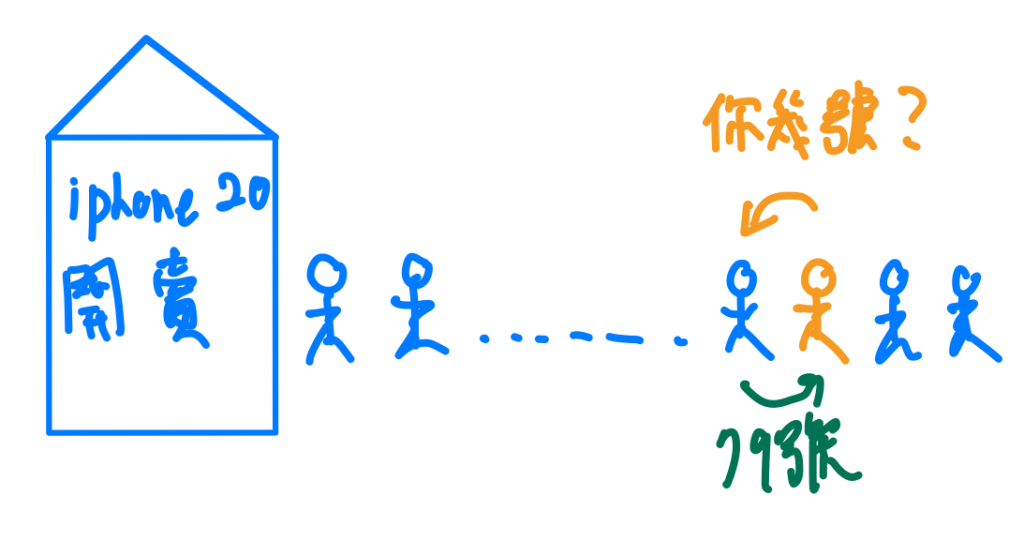
方法二的思想上是不是簡單了許多，但是等等，或許有人會問說，但是我前面那個人也不知道他是在這列隊中的第幾號啊！所以這時候我可以說，我們的問題變成，只要我前面那個人知道他是第幾號，那我就知道我是第幾號囉，所以我前面那個人，又去問了他前面的那個人，他前面的人又去問了他前面的前面的人，這樣的關係會一直持續到甚麼時候呢？答案是一直到「第一個人」！

第一個人總不會不知道他是幾號吧，當第二個人問第一個人說，你是幾號的時候，他就回答我是1號，於是第二個人就把1+1(他自己)等於2這個答案告訴第三個人，第三個人就會告訴第四個人，已此類推，最終你就會知道以自己是幾號了。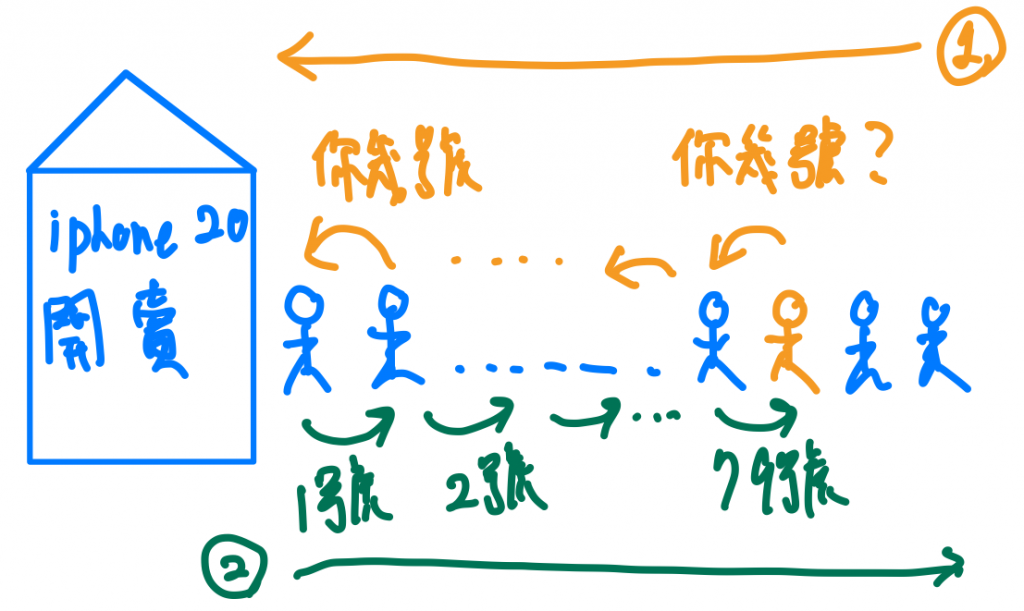

「方法一」就像我們程式裡的迴圈，我們以宏觀的角度去看這個問題，我可以完完全全知道每一次迭代時的狀況。

「方法二」就是遞迴的思想，我們知道我們跟前一層的關係，也知道一定會有一個第一層的base case，我們藉由問前面一個人，讓他一直去往前問直到問到第一個人(base case)後再拿到我們的答案。

現在我們來用以上兩種思考方式來實作階層的函式。

• 第一種我們用遞迴的方式，就像剛剛提到從頭算到我自己是有幾個人這樣，從1開始乘到n。

def factorial(n):
    res = 1
    for i in range(1, n+1):
        res*=i
    return res

• 第二種我們用遞迴的方式，那個if n == 0 就像是我們一直問到第一個人他直接回傳給我們答案，n * fun(n-1)裡面n就是我自己的號碼，fun(n-1)就是我前面那個人的號碼，最終我們也就可以得到一樣的答案。

def factorial(n):
    if n == 0: return 1
    return n * factorial(n-1)

遞迴vs迴圈時間複雜度比較

以這個階層的例子來說，迴圈的時間複雜度很簡單就是O(n)，這邊就不特別介紹了。
而遞迴我們想看看排隊買手機的案例，其實我們是要先一直往前問，到Base Case後再把答案傳回來。所以我們的長度是兩倍也就是O(2n)其實也是O(n)。

為何選擇遞迴？

看完以上例子後，我相信不少讀者會有一個疑問，遞迴那麼難懂，也沒有比較快，為什麼要用遞迴？這邊依我的經驗，我想給出以下幾點。

• 在某些Case下，用遞迴寫會比用迴圈簡單許多。現在大家可能還沒有感覺，之後當我們介紹到跟樹或是圖有關的演算法時，Code的數量就會差很多了。
• 可讀性比較高。當然這個條件取決於團隊內工程師的習慣以及程度。
• 遞迴只需要Focus在當下這個階層時的狀態，他就會幫我做好了。

總結

剛開始接觸遞迴時，我自己覺得相當相當不習慣，但是當我慢慢嘗試去接受他，並且應用在一些演算法時，我才慢慢體會到遞迴的「方便」及「優雅」，有時我還會忘記該怎麼用迴圈去寫一些我覺得是遞迴的問題，所以如果大家有覺得不習慣，不用急~慢慢去思考，有一天就會感受到遞迴能帶給你的便利。