前言

Extended BT，是在我們進入下一章節前 (Huffman algo) 的先備知識，所以先扎根，我們再來往上長！

定義

先來看 Extended 的定義，在一棵二元樹內，我們將原所有 null 的子樹，全部替換成外部點(External nodes)，而我們稱其他的點就為 internal node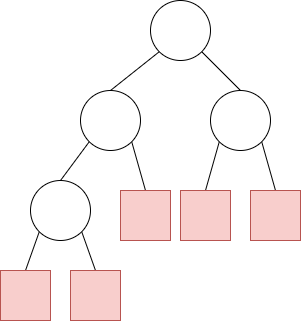

注意看上圖，可以得出 External node = internal node + 1

E=I+2N 定理

在 Extended Binary Tree，有一個我們必須要知道的定理也就是 E=I+2N，我們令
I : 內部各 Node 路徑長的加總
E : 外部各 Node 路徑長的加總
N : Internal node 個數

我們利用數學歸納法來證明

1. 當 N = 0 的時候，I =0，so E = 0
2. 令 N ≤ n-1 時，此式子皆成立
3. 當 N = n 時，將此 B.T 拆成左右子樹

左子樹之內部結點路徑長加總為 ，節點總數
右子樹之內部結點路徑長加總為 ，節點總數
而此 B.T 之 對於真實的 root 來說每個 path 都+1 形成了 nl, nr
而
而我們已知當 N ≤ n-1 的時候式子成立，而左右子樹之 Node 數也 ≤ n-1
所以
代入上式可得
得證