前言

上一章節介紹完 Extended BT，那這邊我們要準備做個延伸，簡短的說明就是把外部節點加上權重，並且定義 WEPL 賦予權重的外部路徑長之加總，而我們想找出最小的 WEPL，即為本章節的 Huffman algo

WEPL (Weight External Path Length)

將 External path 乘上加權後加總，以下圖為例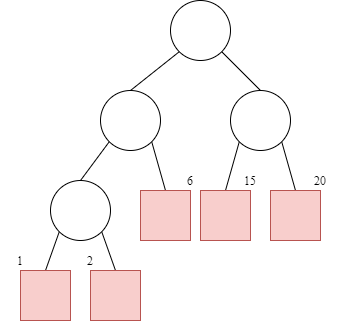

WEPL = 2*(6+15+20) + 3*(1+2) = 91

Huffman Algo

當我們有一個 n 個節點的 BT，可以形成 種 BT，而這些 BT 之中必定會出現具有最小 WEPL 的二元樹，找出他使用的方法就是 Huffman Algo，步驟如下

1. 從加權值集合 W 之中，挑出兩個最小的權重
2. 建立 B.T，並將兩權重加起來放回 W 之中
3. Repeat 1, 2 直到只剩 1 個權值在 W 中 (因此做 n-1次)

如此一來可以建立一棵 Huffman Tree

以下圖來操作

演算法

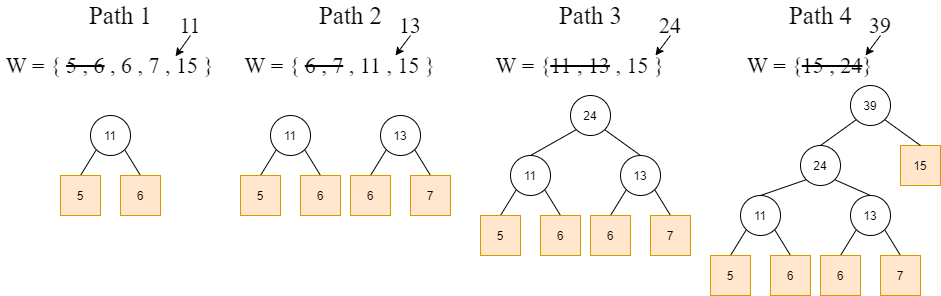
// 假設 node structure [left|weight|right]
huffman(w){
    for i=1 to n-1{
        new(t);
		t->lchild = delete_min(w); // 挑出權重集合W內的最小權重放入左子點
		t->rchild = delete_min(w); // 挑出權重集合W內的最小權重放入右子點
        t->weight = (t->lchild->weight) + (t->rchild)->weight;
        insert(w,t);
    }
}