我們今天來了解FM是怎麼把空間和計算量降下來的

重新看一下，昨天最後的式子

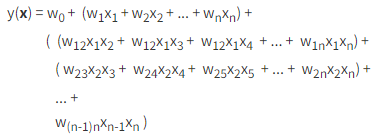
看其中的二階的相加項

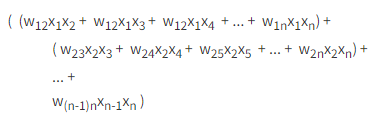
wij 的數目和矩陣的上三角數目很像呀！難道這和矩陣有點關係？

把二階的權重放上對稱矩陣

讓我們來胡思亂想一下，要是我們有一個矩陣 W ，我們把 wij 全放上去，沒定義的地方先寫 0 ，它就變成一個 n x n 維的上三角矩陣（對角線也為0）。

如果再把 wji 的位置設成 wij ，這也就是說 wij = wji， 這表示 i , j 這兩個特徵同時出現時，權重是一樣的，那這個權重矩陣會變成一個對矩陣。

既然出現了對稱矩陣，我們可以用它的一些特性嗎？

如何造出對稱矩陣？

回想一下線性代數的內容，對稱矩陣可以怎樣出現？

若有個矩陣 V ，它的維度是 k x n ，則 V的轉置矩陣 V' 和 V 做內積，則會得到一個 n x n 對稱矩陣。

若我們可以找到 V 使得 V'V 近似於 W，那我們就不用使用 nxn 的空間來存權重了，只要 V 的大小 k x n 就可以了。因為這個 k 我們可以自己設定大小，所以設 k << n 的話，就會比原本的 W 小很多。

當我們要找 wij 時，只要把 V' 的第i個列及 V 的第 j 行做內積，就能算出wij。也就是說：

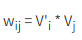
記做 <Vi , Vj>

這要用到的空間，就變成了 O(kn) 而非 O(n^2)

只要能得到 V ，FM的訓練就完成了。

那 V 要怎麼訓練呢？

因為最後的二階的部份，可以寫作以下的式子：

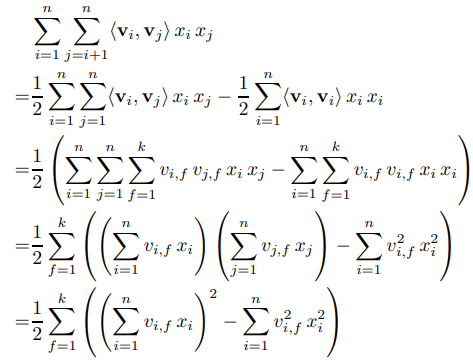
所以一連串的計算以後，我們可以得到

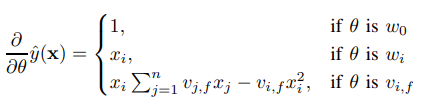
再透過梯度下降法 SGD ，就可以訓練出來了！

參考資料：

FM的論文連結：https://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf