前言

今天要進入的章節是 OBST，那本章節我們先談一些要知道的基本事項，那明天的章節再教大家怎麼求出 OBST，大家要先釐清本章節的概念，不然在接下來的推導過程中，會很容易就迷失方向唷 QQ

前情提要

之前在談 BST 的章節曾經有提到，BST 會因為輸入元素的順序不同，而長成不同形狀、種類的 BST，所以我們這邊要先理解一件事，當我們談到 BST，其實他是可以擁有很多不同長相的，而有多少種類呢？之前也有提到數量 =

簡單介紹

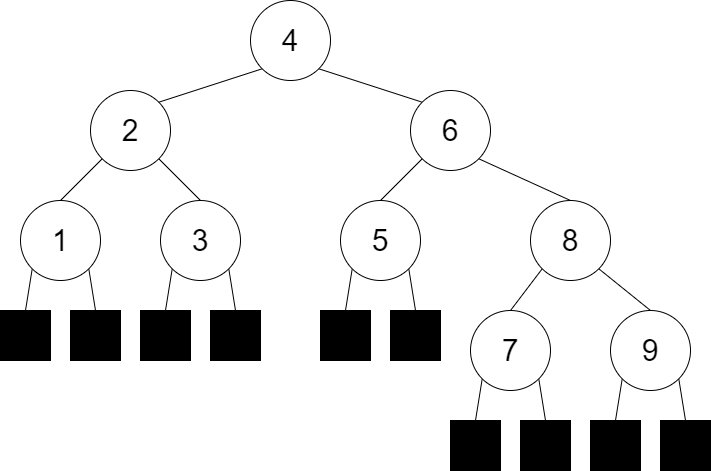
讓我們先看上面這張圖，擁有 n=9 個內部節點，必然會創造出 n+1 = 10 個失敗節點
我們再為這些內部、失敗節點都賦予一個加權值 ( 內部 pi 失敗 qj ) 先假設加權值都為1 (實際上不一定)
這邊先定義以下幾件事情

1. 成功搜尋成本 = 內部節點的level值 * pi 我們要的是比較次數
2. 失敗搜尋成本 = (失敗節點的level值-1) * qi 我們要的是比較次數
3. 搜尋總成本 = 成功搜尋成本 + 失敗搜尋成本

若以上圖為例的話，這棵 BST 的搜尋總成本就是 (1 + 2 * 2 + 3 * 4 + 4 * 2) + (3 * 6 + 4 * 4) = 59
而組成這棵 BST 的節點，像前情所提到的，當然還可以成為各種其他不同的 BST，而我們要找的OBST，就是這群BST中搜尋總成本最小的BST

採取方法

我們要採取的方法是使用 Dynamic Programming 的概念

1. 先去定義出 Solution 的公式
2. 設立 table 來記錄子問題的 solution
3. 重複使用這些子問題的結果
   最終來完成我們的大問題

明日預告

下一章節再來談怎麼定義 Solution 公式，還有把如何求出 OBST 的方法教給大家啦，辛苦ㄌ辛苦辛苦辛辛苦苦