Best Time to Buy and Sell Stock II

題目說明

給定一個價錢數列，prices[i]代表第i天的股票價錢。
需求是求出最大利潤，一次只能持有一張股票，但可以隨買隨賣，即允許今天賣掉馬上又買

範例

Example 1:
Input: prices = [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.

Example 2:
Input: prices = [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.

Example 3:
Input: prices = [7,6,4,3,1]
Output: 0
Explanation: There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.

限制條件和特別需求

• 1 <= prices.length <= 3 * 10^4
• 0 <= prices[i] <= 10^4

思路

這題應用到Greedy(貪婪演算法)，詳可見維基百科
簡單來說，就是每一步都貪心的選擇最好答案(局部最佳解)，那結果就會是最好的(全局最佳解)

根據此演算法理論，每一天是否有正利潤(有的話就是局部最佳解)，加總每一天的正利潤就得到最大利潤(全局最佳解)。
畫成下圖更容易了解，紅色部分全部加起來就是。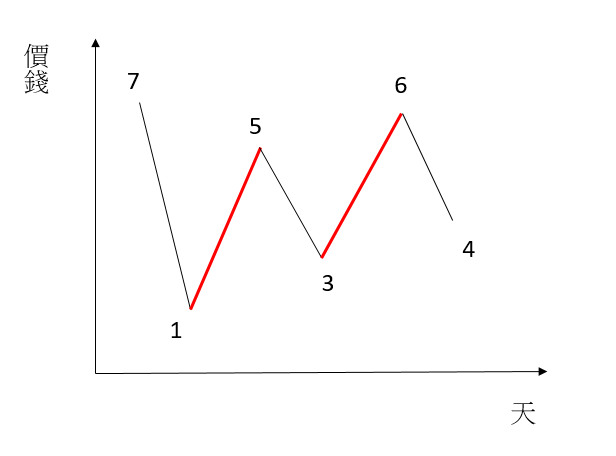

C++ 程式碼

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int maxProfit = 0;
        for (int i=1; i<prices.size(); i++) {
            if (prices[i] > prices[i-1])
                maxProfit += prices[i] - prices[i-1];
        }
        return maxProfit;
    }
};

Python3 程式碼

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        maxProfit = 0
        for i in range(1, len(prices)):
            if prices[i] > prices[i-1]:
                maxProfit += prices[i] - prices[i-1]
        return maxProfit