在卷積神經網路出現以前，最常見的神經網路就是MLP（多層感知機，Multi-Layer Perceptron）了。這種神經網路至少包含三層（輸入層、隱藏層以及輸出層），並且相鄰層的節點為全連接，也就是每一層的節點會連接到下一層的所有節點。

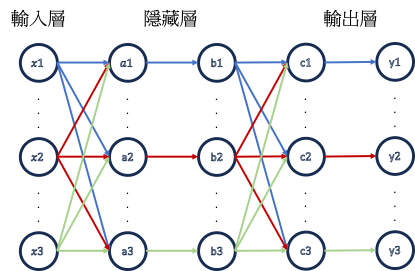
模型在運作時會根據節點之間的權重以前向傳遞（Forward Propagation）的方式去做運算，從輸入層根據權重運算傳遞至下一層，不斷重複直到在輸出層得到結果。而在模型訓練時，便是在訓練這些權重，模型會以反向傳遞（Backward Propagation）的方式從輸出層向前做運算，以多微分方程得到結果。

前向傳遞（Forward Propagation）

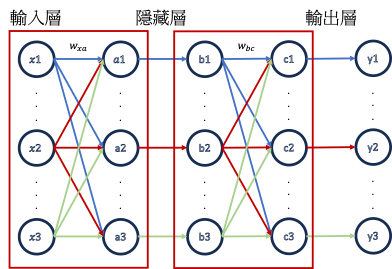
模型在運作時，會將節點內的數值經由權重相乘後再加總往下傳遞，就如上圖輸入層傳遞至隱藏層以及隱藏層傳遞至輸出層時所做之運算。

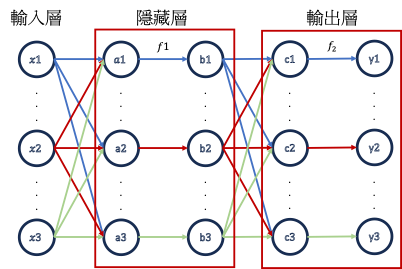
而在節點運算完過後，會再經過激勵函數得出最終的值才賦予節點。

反向傳遞（Backward Propagation）

反向傳遞會從模型的最後一層根據error function以及運用微積分的chain rule來進行回推，最終計算出各個節點之間所連接的權重。由於計算過程運用到微積分以及過程過於繁瑣，如果要詳細說明會用掉過多篇幅，因此筆者在這邊先不多作介紹，有興趣的讀者可以自行查詢實際運算方式以及過程。

激勵函數（Activation Function）

最後介紹幾款常用的激勵函數。
（1） ReLU（Rectified Linear Unit）

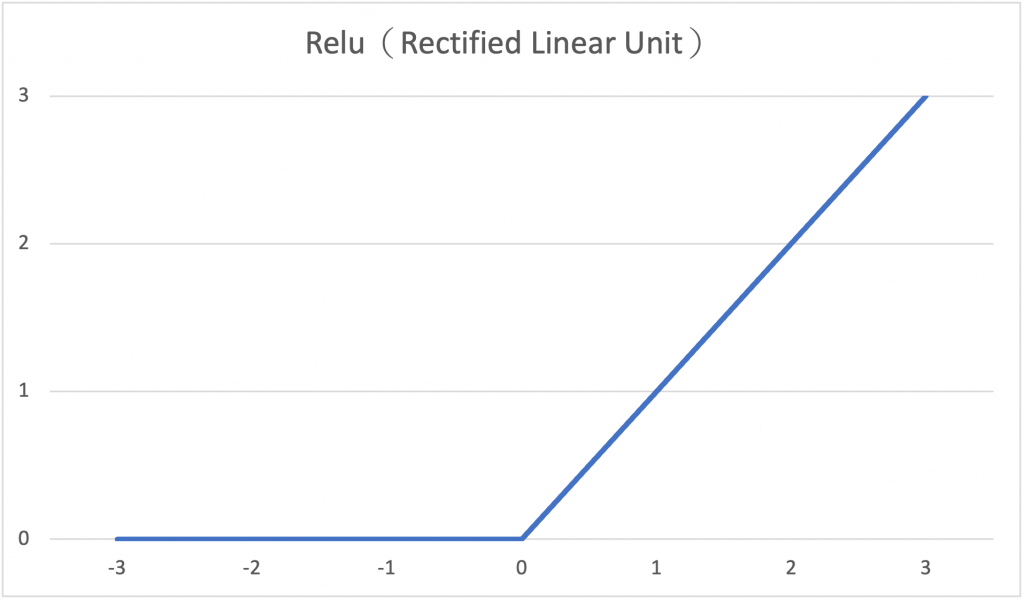
ReLu函數的輸入值若為正數，則輸出不變；若為負數則輸出為0。使用ReLU做為激勵函數可以減緩過度擬合（overfitting）以及梯度消失、梯度爆炸的問題。

（2）Sigmoid

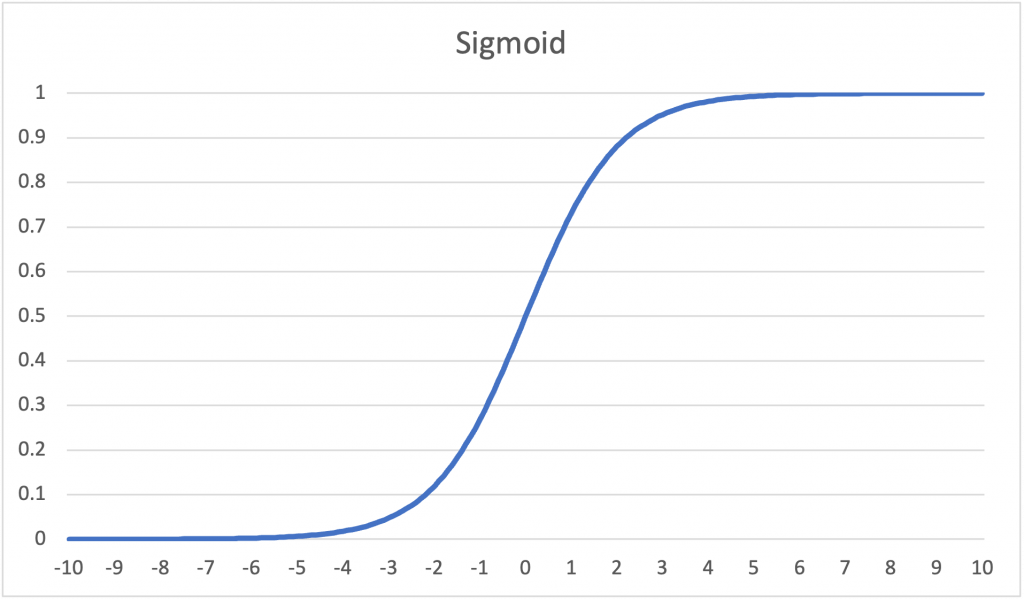
Sigmoid函數適用於二元分類，但當輸入值具有離群值時，Sigmoid無法反映出來，並且具有梯度消失的潛在風險。

（3）tanh

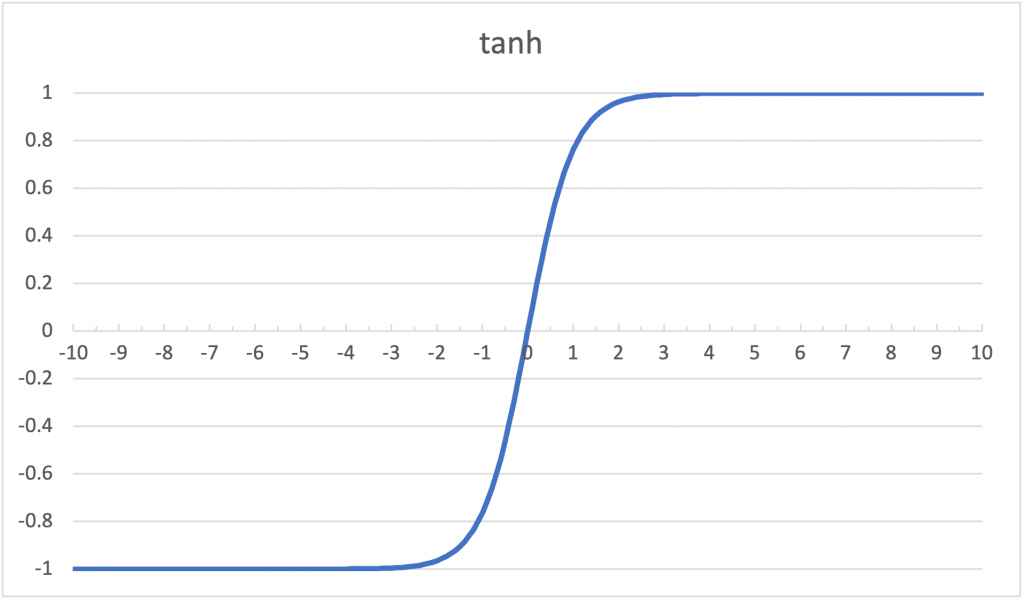
tanh函數圖形與Sigmoid函數圖形相似，但其範圍為[-1, 1]，其收斂速度比Sigmoid函數快，但也具有梯度消失的潛在風險。

（4）Softmax

=\frac{e^{x_{j}}}{\sum_{k=1}^{K}e^{x_{k}}}\ for\ j=1,2,...,k)

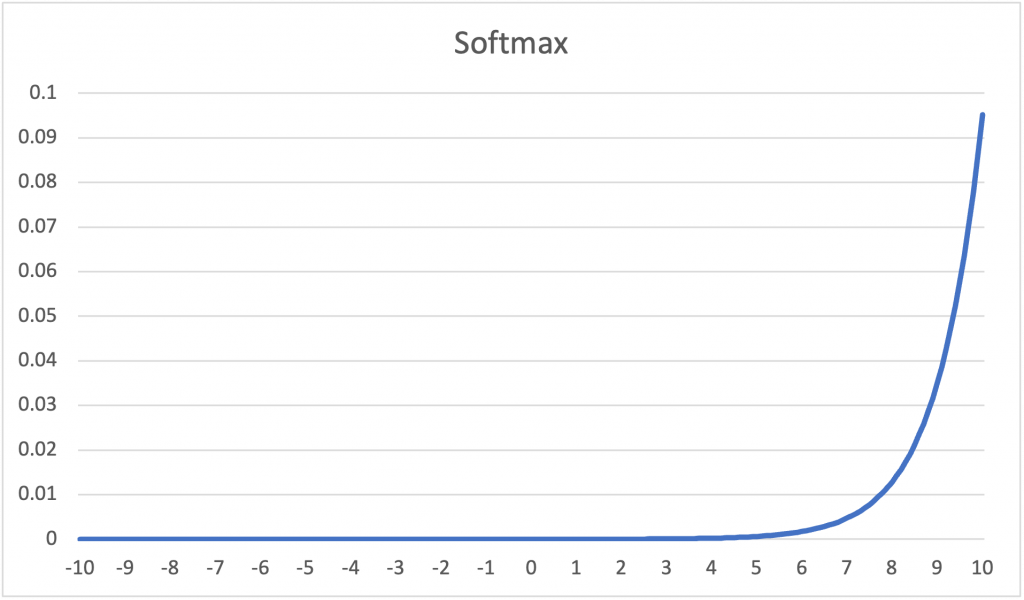
Softmax函數適用於多元分類問題，但遇到離群值時，輸出值會更加偏離，因此建議不要用在複雜的影像辨識之中。