開賽第四天已經開始苟延殘喘了QQ

持續在區間求和的路上往前邁進，這系列應該頂多再介紹一兩天就可以小結了喔耶。

今天讀的是樹狀數組 (binary indexed tree/BIT)，這邊的 binary 不是 binary tree，而是指二進位。簡單的示意圖如下：

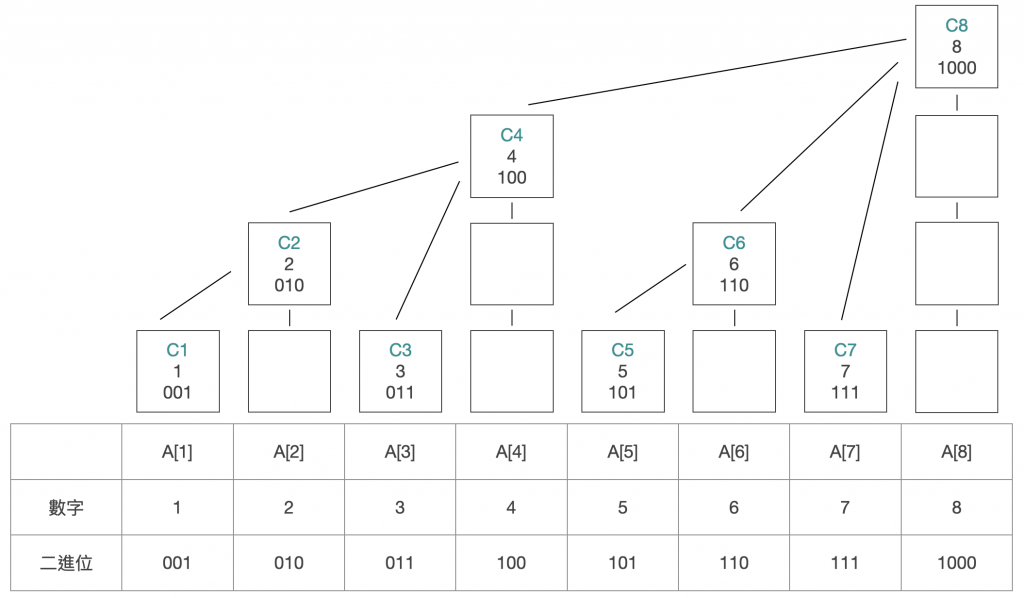
把數字用二進位表示，最底層的 leaf node 最後一個 bit 是 1，然後上面一層是倒數第二個 bit 是 1，這樣每個數字用 bit 表示，根據最末位的 1 來決定位置。而某個數字的父節點，會是加上自己最後一位的 1，例如 6 是 110，父節點就是 110+010=1000=8。

在算法中，我們可以用 x & -x 來取得最後一個二進位表示的 1（以及後面的 bit）。假設有最末位為 1 和最末位不是 1 的情況，由於 -x 是 x 的補數+1，所以把兩個做 bitwise and 就可以得到最後一位的 1。

但是為什麼要找最末位的 1 呢？這就和區間和有關了。

• 概念一：A(i)~A(j) 的區間和會是 [A(1)~A(j)] - [A(1)~A(i-1)]
• 概念二：A(1)~A(n) 的區間和可以依照 bit 被拆掉，例如 13=1101，所以 A13 = B(1101)+B(1100)+B(1000) = B(13)+B(12)+B(8)，每次會拔掉最右邊的 1 直到拔光為止，詳細圖解可以看這裡比較清楚，下面則是簡易版規則圖

以上是關於樹狀數組的簡單說明，把這些概念都轉成程式碼就是解法了。

class NumArray:
    def __init__(self, nums: List[int]):
        self.nums = nums
        self.tree = [0] * (len(nums) + 1)
        for i, num in enumerate(nums, 1):
            self.add(i, num)

    def add(self, index: int, val: int):
        while index < len(self.tree):
            self.tree[index] += val
            index += index & -index

    def prefixSum(self, index) -> int:
        s = 0
        while index:
            s += self.tree[index]
            index &= index - 1
        return s

    def update(self, index: int, val: int) -> None:
        self.add(index + 1, val - self.nums[index])
        self.nums[index] = val

    def sumRange(self, left: int, right: int) -> int:
        return self.prefixSum(right + 1) - self.prefixSum(left)

• binary index tree

  • 307. Range Sum Query - Mutable(大概看懂了但還沒寫完QQ)

• 參考資料

  • YUI HUANG 演算法學習筆記(這篇很詳細)
  • WIWIHO 的競程筆記