前言

此篇主要為Writeup跟 . . . 相關筆記，會解以下兩題，gogo!

Writeup

Modular Arithmetic 1

題目

網址 : https://cryptohack.org/courses/modular/ma0/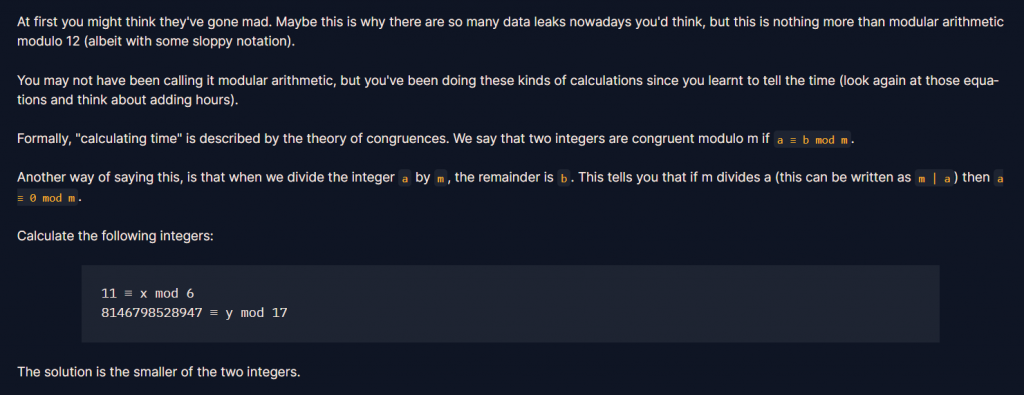

思路

舉例 : 34 ≡ 18 mod 4 就是「 34跟18在除以4的情況下，有相同的餘數」
所以題目第一列 11 ≡ x mod 6 就是「11跟x在除以6的情況下，有相同的餘數」
代表此式子也可以寫成x ≡ 11 mod 6，11 % 6 = 5，所以x = 5
第二列 8146798528947 ≡ y mod 17 ，8146798528947 % 17 = 4，y = 4
最後題目要x, y的最小值

解法

• code

# 11 ≡ x mod 6
# 8146798528947 ≡ y mod 17

x = 11 % 6
y = 8146798528947 % 17
print(f"x, y min : {min(x, y)}")

• output
  

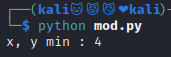
flag : 4

Modular Arithmetic 2

題目

網址 : https://cryptohack.org/courses/modular/ma1/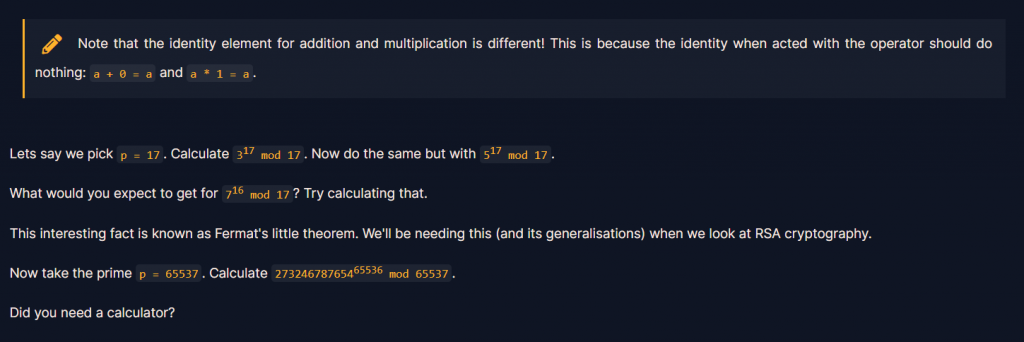

思路

題目為 : p = 65537， 273246787654^65536 mod 65537
利用費馬小定理(Fermat's little theorem)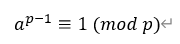

發現可代入題目 a = 273246787654, p = 65537, p-1 = 65536
代表說 「a跟1在除以p的情況下，有相同的餘數」1%65537 = 1
所以餘數為1

解法

1%65537 = 1

flag : 1

統整

• 費馬小定理（Fermat's little theorem）

1. 假如a是一個整數，p是一個質數，那麼a^p - a是p的倍數，可以表示為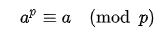
   

2. 如果a不是p的倍數，這個定理也可以寫成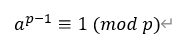
   

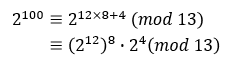
   • 舉例 : 計算 (2^100) / 13的餘數
     

     根據上面第二點設a = 2, p = 13，(2^12)^8可以寫成
     

   
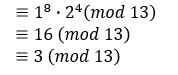
   所以餘數為3
   完整如下 : (來源 : https://zh.wikipedia.org/zh-tw/%E8%B4%B9%E9%A9%AC%E5%B0%8F%E5%AE%9A%E7%90%86#%E5%8E%86%E5%8F%B2)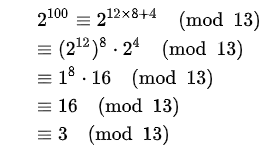
   

證明有興趣的話可上網查看

小結

今天學到了費馬小定理的應用，第一次使用它，發現挺好用的!而且之後在RSA好像也會用到，所以要熟悉!先到這裡拉，明天繼續模運算!

參考資料

模運算 : https://zh.wikipedia.org/zh-tw/%E6%A8%A1%E7%AE%97%E6%95%B8

費馬小定理 : https://zh.wikipedia.org/zh-tw/%E8%B4%B9%E9%A9%AC%E5%B0%8F%E5%AE%9A%E7%90%86#%E5%8E%86%E5%8F%B2

[離散數學] 費馬小定理 : https://ithelp.ithome.com.tw/articles/10205906