前言

在神經網路中，通常會讓每層的神經元輸出後再經過激勵函數，它對於神經網路的性能扮演著重要的角色，主要是利用激勵函數的下列特性：

• 引入非線性：我們知道神經元其實就是個基於權重和偏差的線性函數，在神經網路中，無論加入多少層隱藏層，多個線性函數 ( 神經元 ) 組合起來最後也是線性函數，能夠處理的問題也就較單一，但加入了激勵函數後，能把輸出的線性函數轉為非線性函數 ( Non-linear Function )，經過這個神經網路訓練出來模型就能處理更複雜的任務和特徵
• 分類問題：激勵函數在分類問題能夠將神經網路的輸出經過非線性轉變為機率的形式，使得神經網路能夠預測屬於不同類別的機率，讓神經網路能夠更好的分類，解決了無法用線性分類的問題，下圖左是用線性函數 ( 綠線 ) 來劃分類別，適用在較簡單的問題，但如果是下圖右較複雜的情況下要劃分類別，就需要用非線性函數來劃分

• 反向傳遞的計算：反向傳遞會用到激勵函數的導數來計算梯度，以更新模型的參數，使得不同激勵函數的選擇會至關重要。
• 處理不確定性：在分類任務中，對於屬於某個類別的機率可能需要考慮多種特徵的組合，這時就需要非線性的激勵函數來應付這種不確定性

常見的激勵函數

神經網路中有許多不同的激勵函數，其特點和使用的時機都不相同，下面是一些常用的激勵函數：

Sigmoid 函數

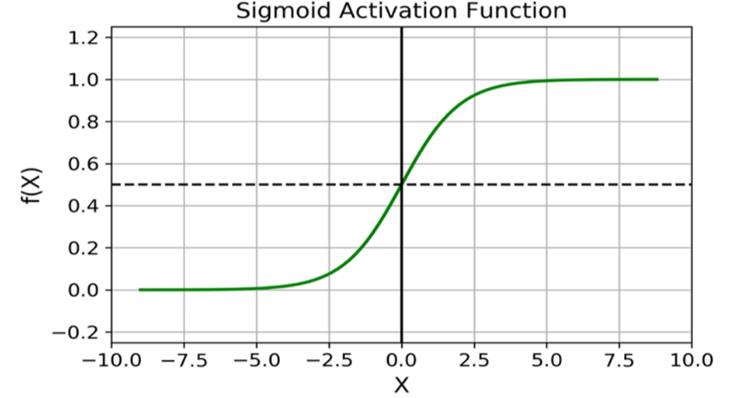
Sigmoid 函數 是個平滑的 S 型曲線，為非線性函數，常用在神經網路中的隱藏層和輸出層作為神經元的最後輸出， 如下：

• 取值範圍：Sigmoid 函數的取值範圍在 ( 0 , 1 )，這使它可以將神經元的輸出轉變為介於 0 和 1 之間屬於某個類別的機率，在二元分類的問題中就很常被拿來使用，在用最後 的值用閥值去判斷輸出 1 還是 0
• 平滑性質：Sigmoid 函數相對較平滑，這對進行反向傳遞計算導數或梯度時有利，但若 的值趨近於 0 時，因為反向傳遞時會梯度會不斷累乘，當不斷乘上趨於 0 的值時，梯度會越乘越小，最後可能會導致梯度消失 ( Vanishing Gradient ) 的問題使得神經網路難以學習
• 下面為 的導函數，可以發現輸入 逐漸的往正向增加或往負向增加，微分後的結果皆會接近 0：

ReLU 函數

ReLU 函數會使當輸入的值大於 0 時，輸出就為輸入值，如果輸入值小於 0 時，輸出一律為 0，公式為：

Sigmoid 與 ReLU 的選擇

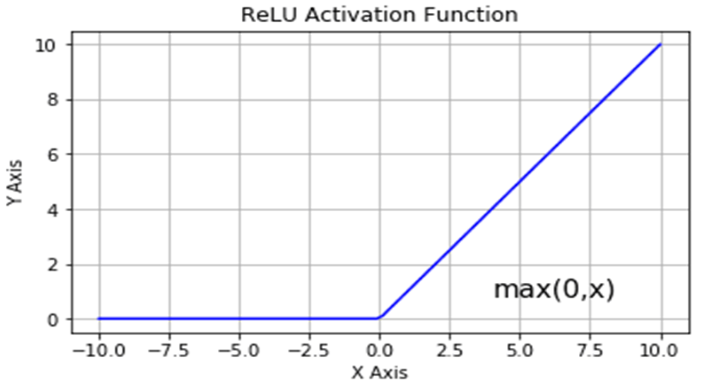
ReLU 函數較簡單，計算效率也較高，避免了剛才 Sigmoid 函數所會遇到的梯度消失問題，因為Sigmoid 函數的導函數為 ，表示輸入 不管是正數還是負數， 導數都趨於 0，這會在反向傳遞中進行連鎖率計算時，因為梯度的不斷相乘而導致梯度消失，但 Relu 函數在輸入 為正數時，導數恆為 1，因此就兩個函數在 為正數的情況下來說，Relu 能在反向傳遞中較好的保持梯度大小，不會有梯度消失的問題，考慮到計算效率和梯度問題，目前也較常使用 ReLU 函數作為神經網路的激活函數。

神經元死亡問題 Dying ReLU Problem

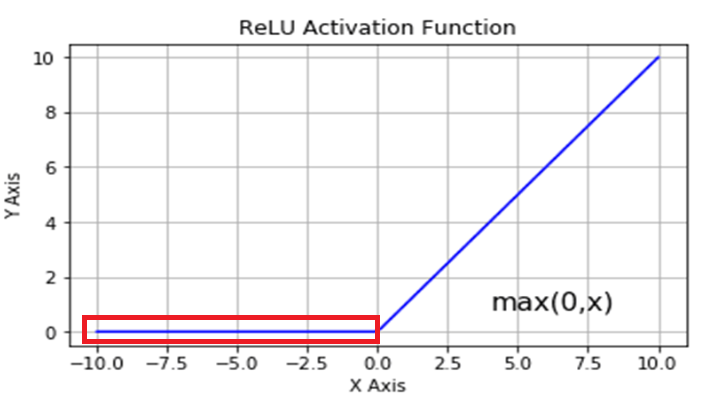
但可以發現到，Relu 在輸入 為負數時，不管為負多少，神經元輸出會一直保持為 0，反向傳遞時因為梯度一直為 0，導致這種情況下參數無法更新學習，即使其它的參數學習得很好，最後還是只能停在原地無法再變更好，這就是所謂的神經元死亡問題。

Softmax 函數

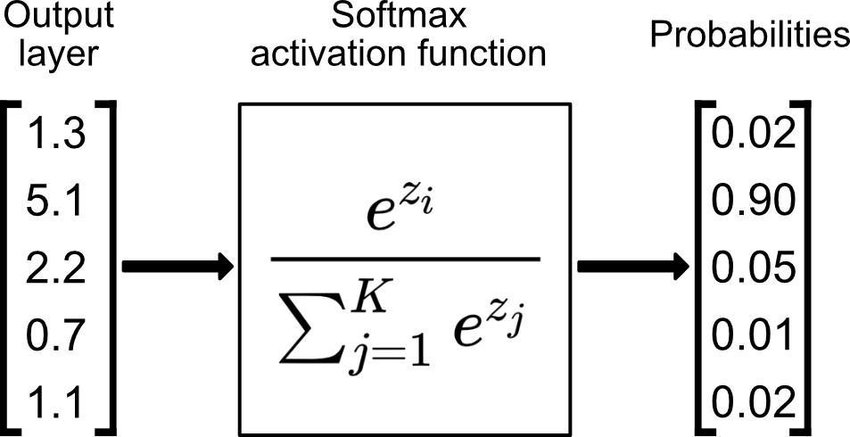
在神經網路中，Softmax 函數通常會使用在輸出層，將原始的輸出向量轉變為類別的機率分布，在多元分類問題中，要分類 個類別的話，輸出層 ( Output layer ) 最後就會輸出 個值的向量，Softmax 函數會將這向量中的值轉換成介於 0 和 1 之間的機率，也就是對映到屬於不同類別的機率，並且會讓所有類別的機率加總和為 1，整個轉換過程與 Softmax 函數公式如下：

Tanh 函數

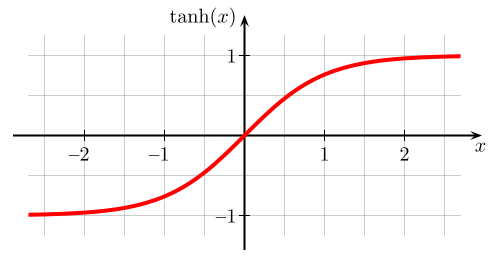
Tanh 函數和 Sigmoid 函數長得有點像，但 Tanh 函數的範圍介於 ( -1 , 1 )，其值域更加廣 ，能夠讓神經網路處理正或負的輸入資料，但因為函數範圍大小的關係，輸入值在較大或較小的情況下，在反向傳遞計算時仍有梯度消失的問題，Tanh 函數公式如下：

不同的激勵函數適用在不同的任務和場合，面對到反向傳遞時計算的效率也不盡相同，激勵函數的選擇也會影響著神經網路學習的速度與效能。

小結

今天我們學到：

• 各種激勵函數功能與特性
  • Sigmoid 函數
  • ReLU 函數
  • Softmax 函數
  • Tanh 函數

我們前幾天有提到單一感知器 ( Perception ) 與多層感知器 ( Multilayer Perception ) 的區別，若我們要讓模型經過更複雜的訓驗，神經網路就會變成多層感知器 ( Multilayer Perception ) 的形式，即為深度神經網路 ( Deep Neural Network , DNN )，並根據其特性進行所謂的深度學習 ( Deep Learning )，下篇文章就會針對深度神經網路的架構與概念進行介紹，那我們下篇文章見 ~

參考資料

https://machinelearningmastery.com/a-gentle-introduction-to-sigmoid-function/

https://www.nomidl.com/deep-learning/what-is-relu-and-sigmoid-activation-function/

https://www.researchgate.net/figure/Working-principles-of-softmax-function_fig3_349662206

https://commons.wikimedia.org/wiki/File:Hyperbolic_Tangent.svg