前言

其實模型就是個函數，為特徵資料的線性函數，用來表示特徵 ( 輸入 ) 與目標 ( 輸出 ) 之間的關係，但這個函數顯然太過簡單，需要在表示成複雜一點的函數，模型才會比較成熟，效能才會較好，至於要怎麼讓函數更加複雜，就會用到今天的主角 - ANN 人工神經網路 ( Artificial Neural Networks , ANN )，人工神經網路就像是由多的神經元組合成的網路，ANN 就是利用神經元相互傳遞訊息的功能來實現函數複雜化。

神經元 Neuron

下面來了解一下神經元的重要部位以及特性：

• 樹突 Dendrite：用來接收傳入的訊息
• 細胞體 Cell body：神經元的主要結構，用來處理接受到的訊息
• 軸突 Axon：作為一個神經元的輸出，負責給其他的神經元傳遞訊號
• 突觸 Synaptic terminals：作為軸突的末梢，與其他神經元的樹突產生連接，進而傳遞訊號

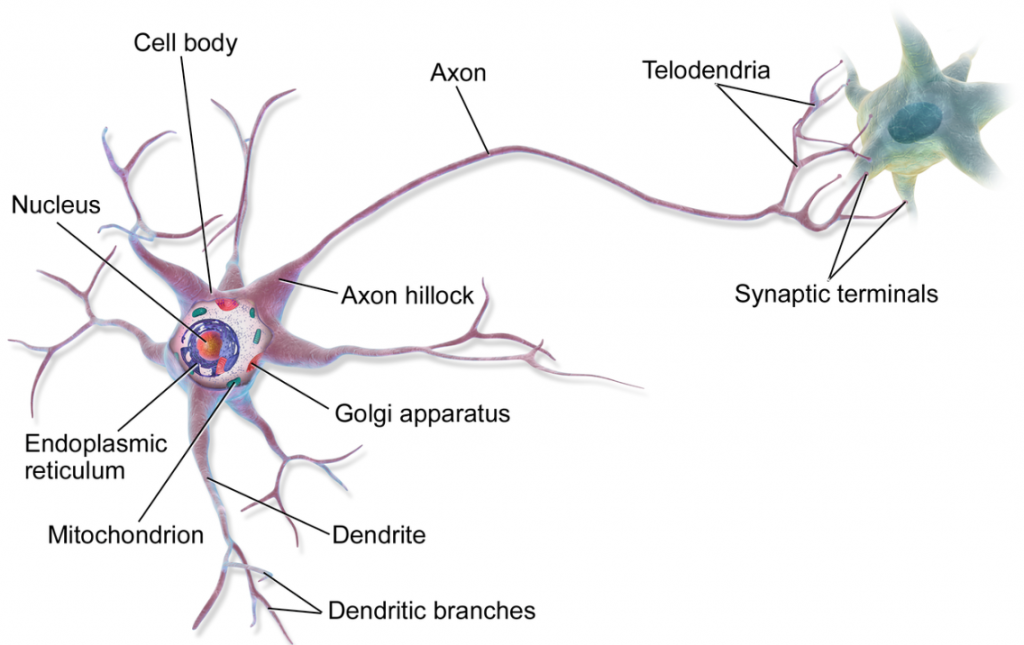
對於神經元的運作流程：先從樹突接收其他神經元傳入的訊息 → 透過細胞體進行訊息處理 → 經過軸突再經過突觸與其他神經元連接把訊息傳遞出去，而 ANN 就是模擬整個生物的神經系統運作流程，透過無數的神經元相連而成，能夠在接收到外界傳入刺激後迅速傳達訊息做出反應。

感知器 Perception

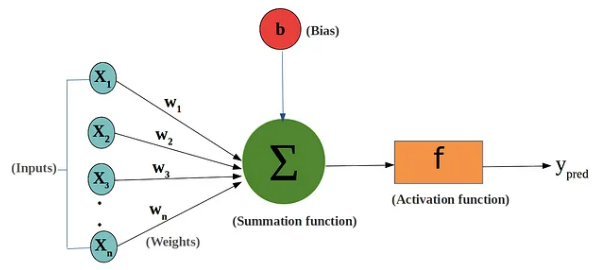
感知器的基本組成元件：

• 權重 ( Weights , )：每個輸入特徵 都會對映到一個相關的權重 ，這些權重就是用來調節每個特徵資料的重要性
• 偏差 ( Bias , )：每個感知器都會有一個偏差，可以調整輸入特徵和權重的線性組合
• 激勵函數 ( Activation function , )：判斷感知器的輸出要激勵 ( 輸出為 1 ) 還是不激勵 ( 輸出 0 )，如果大於閥值就激勵，否則不激勵，最常和閥值函數搭配使用，激勵函數就是透過本身的非線性將線性函數 進行轉換

感知器也稱為神經元，就是一種具有二元分類功能的簡單函數，在邏輯回歸任務中感知器利用激勵函數 Sigmoid 函數將輸入的線姓函數 值轉換成一個機率值 ，其大小在 0 和 1 之間，最後再經過閥值函數把輸入的線性函數轉成 0 或 1，閥值函數的功能就是透過判斷 是否大於一個閥值 ( threshold )，大於的話 就為 1 輸出，否則為 0。

感知器的計算步驟如下：

1. 加權計算：將 個輸入的特徵 分別乘上各自的權重 再全部加起來最後加上偏差得到 ，得到下面公式：

1. 激勵函數：把算出來的 傳入激勵函數計算後得到 ，再經過閥值大小的判斷就計算出了一個感知器的輸出

如果有學過線性代數的話，就會發現感知器會先透過權重 對輸入的 進行兩矩陣的相乘運算，再根據相乘後的結果判斷是否有超過閥值來輸出 1 和 0。

多層感知器 Multilayer Perception

多層感是一種由多個神經元所組成的人工神經網路，它是對單一感知器的擴展，能夠處理更複雜的問題，單一感知器僅為單層的簡單線性組合，可以看成整個神經網路只存在輸入層和輸出層，而多層感知器就藉著神經元彼此互通的特性，每個感知器都有一個輸入，這個輸入是由上一層的神經元的輸出（乘以權重）經過加權總和得到的，激勵函數會對這個加權總和進行處理，並產生輸出。這個輸出將被傳遞到下一層的神經元，進行進一步的處理，一層一層的傳下去，這使得多層感知器可以表示非常複雜的函數，ANN 就是透過這樣的方式，將很多的神經元 ( 感知器 ) 做函數的複合，最後把所有的神經元都串接起來形成人工神經網路，最後的輸出的就會是一個複雜的複合函數 ：

感知器，通常是單層神經元的簡單組合。它可以看成是一個只有輸入層和輸出層的多層感知機，用來解決簡單的二元分類問題。多層感知機在感知機的基礎上加入了隱藏層，能夠處理更複雜的模式和任務。

小結

今天我們學習到：

• 人工神經網路的組成與特性
• 神經元的特性
• 權重與偏差的計算
• 感知器與多層感知器

我們知道每個神經元，也就是感知器，最後輸出前都會經過一個特別的函數 - 激勵函數 ( Activation Function )，它讓模型能夠以非線性的樣貌去應付更加複雜的問題，明天我們會針對這個函數進行介紹，那我們就下篇文章見 ~

參考資料

https://www.javatpoint.com/perceptron-in-machine-learning

https://towardsdatascience.com/whats-the-role-of-weights-and-bias-in-a-neural-network-4cf7e9888a0f

https://en.wikipedia.org/wiki/Neuron