前言

今天此篇為把之前新學到的定理做統整，內容包含模運算、歐幾里得算法、擴展歐幾里得算法、費馬小定理、二次剩餘、中國剩餘定理

統整

---------------

模運算

表示為𝑎 𝑚𝑜𝑑 𝑛 ，𝑎代表被取模的數，𝑛是模數，運算結果為𝑎除以𝑛的餘數

e.g. 18 mod 4 = 2 因為18除以4的餘數為2

• 同餘關係
  如果𝑎, 𝑏 兩數除以同一個數𝑛，餘數相同，且兩數的差值𝑎 − 𝑏為 𝑛 的整數倍，就可以說𝑎跟𝑏在模𝑛下的時候同餘
  並用 𝑎 ≡ 𝑏 (𝑚𝑜𝑑 𝑛) 表示

  e.g. -8 ≡ 7 (𝑚𝑜𝑑 5) 、 5 ≡ 7 (𝑚𝑜𝑑 2)

• 運算定律

𝑎≡𝑏 (𝑚𝑜𝑑 𝑛) ， 𝑝≡𝑞 (𝑚𝑜𝑑 𝑛)， 𝑐為任何正整數

𝑎 + 𝑐 ≡ 𝑏 + 𝑐 (𝑚𝑜𝑑 𝑛)
𝑎 − 𝑐 ≡ 𝑏 − 𝑐 (𝑚𝑜𝑑 𝑛)
𝑎 ∙ 𝑐 ≡ 𝑏 ∙ 𝑐 (𝑚𝑜𝑑 𝑛)
𝑎^𝑐 ≡ 𝑏^𝑐 (𝑚𝑜𝑑 𝑛)
𝑎 + 𝑝 ≡ 𝑏 + 𝑞 (𝑚𝑜𝑑 𝑛)
𝑎 ∙ 𝑝 ≡ 𝑏 ∙ 𝑞 (𝑚𝑜𝑑 𝑛)

• 模反元素
  • 存在條件 : 整數a與模數n互質
  • 公式
    

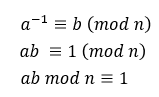
  b為a的模反元素

  • 求模反元素的方式(設整數 = a, 模數 = n, a的模反元素 = b)

    • Fermat's little theorem(限定模數要為質數，在此模數 = p)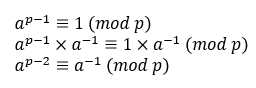
      
      b = a^(p-2) % p

    • Extended Euclidean algorithm
      設𝑒𝑥𝑔𝑐𝑑(𝑎, 𝑛)為擴展歐幾里得算法的函數，可得
      𝑎𝑥+𝑛𝑦=𝑔 ， 𝑔=𝑔𝑐𝑑(𝑎, 𝑛)(最大公因數)

      • 𝑖𝑓 𝑔 = 1
        代表該模反元素存在，且𝑎𝑥+𝑛𝑦= 1
        𝑎𝑥+𝑛𝑦 ≡ 𝑎𝑥 ≡ 1 (𝑚𝑜𝑑 𝑛)
        模反定義 :𝒂 ∙ 𝒂^(−𝟏) ≡ 1
        由此可知，𝑥為𝑎模𝑛的其中一個模反元素
      • 𝑖𝑓 𝑔 ≠ 1
        則該模反元素不存在

    • python Crypto.Util.number函式庫中的inverse

    from Crypto.Util.number import inverse
    b = inverse(a, n)
    

---------------

歐幾里得算法 - Euclidean algorithm

• 輾轉相除法，來源：https://www.csie.ntu.edu.tw/~b98902112/cpp_and_algo/cpp02/euclidean_algorithm.html)
  
  34先跟10除，得到餘數4後10再去跟4除，得到餘數2後再去跟4除，最後得到0結束
  設兩數a, b 且a > b, 商為q, 餘數為r, mod用"%"代替
  輾轉流程(讓a永遠都是被除數) :

1. r = a%b
2. a = b
3. b = r
4. 如果b為0就結束，否則回到第1點
5. 最後b為兩數最大公因數

以下為code實現

• code_1

while(b != 0):
    temp = a % b
    a = b
    b = temp
print(a)

• code_2

import math
print(math.gcd(a, b))

---------------

擴展歐幾里得算法 - Extended Euclidean algorithm

• 擴展輾轉相除法
  a * u + b * v = gcd(a,b)，利用此算法求u跟v
  貝祖定理 : ax + by = gcd(a, b)
  過程 : (來源 : https://ccjou.wordpress.com/2012/11/16/%E5%88%A9%E7%94%A8%E5%9F%BA%E6%9C%AC%E5%88%97%E9%81%8B%E7%AE%97%E5%AF%A6%E7%8F%BE%E6%93%B4%E5%B1%95%E6%AD%90%E5%B9%BE%E9%87%8C%E5%BE%97%E6%BC%94%E7%AE%97%E6%B3%95/)
  

以下為code實現

• code_1

from egcd import egcd
print(egcd(a,b))

---------------

費馬小定理 - Fermat's little theorem

1. 假如a是一個整數，p是一個質數，那麼a^p - a是p的倍數，可以表示為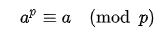
   

2. 如果a不是p的倍數，這個定理也可以寫成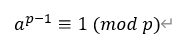
   

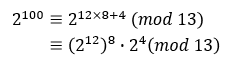
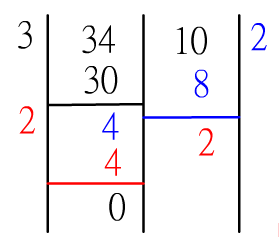
   • 舉例 : 計算 (2^100) / 13的餘數
     

     根據上面第二點設a = 2, p = 13，(2^12)^8可以寫成
     

   
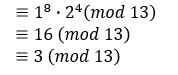
   所以餘數為3
   完整如下 : (來源 : https://zh.wikipedia.org/zh-tw/%E8%B4%B9%E9%A9%AC%E5%B0%8F%E5%AE%9A%E7%90%86#%E5%8E%86%E5%8F%B2)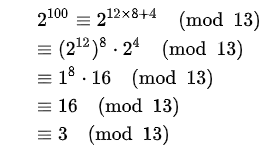
   

---------------

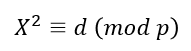
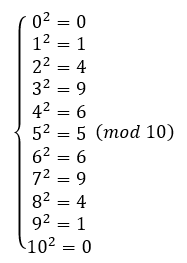
二次剩餘 - Quadratic Residues

• 任意非零平方整數除以某個數後可能的餘數，我們稱之為「二次剩餘」
  • 
  • 成立時，稱d是模p的二次剩餘(quadratic residue)
  • 不成立，稱d是模p的二次非剩餘(non-quadratic)
  • 計算方式
    • X^2 % p = d
  • 例子!
    • mod 10(左邊為X，右邊為d(二次剩餘))
    • 

    1^1%10 = 1, 2^2%10 = 4, 3^2%10 = 9, 4^2%10 = 6, 5^2%10 = 5...

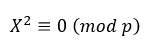    • 由此可知，對於模10而言，可能的餘數集合為{0, 1, 4, 5, 6, 9}，因為通常 都有解，所以不考慮0。所以在此，模10的二次剩餘為{1, 4, 5, 6, 9}
• 勒讓得符號 Legendre Symbol
  • (a / p) ≡ a^((p-1)/2) mod p
  • 
    • (a|p) = 1，a 為二次剩餘(mod p)
    • (a|p) = −1， a 為二次非剩餘(mod p)

---------------

中國剩餘定理 - Chinese remainder theorem

• 假設整數m1, m2, ... , mn其中任兩數互質，則對任意的整數：a1, a2, ... , an，方程組S有解
  
  • 求通解步驟(在此舉例有3個式子)
    
    • 先求M = m1 * m2 * m3
    • M1 = M//m1, M2 = M//m2, M3 =M//m3

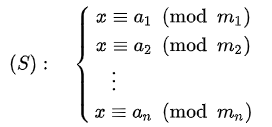
    e.g. a = 5 // 2, a = 2, 由此例子可知" // " 意思為除後取整數商的部分

    • 求M1, M2, M3的模反元素，分別為t1, t2, t3
    • 最後通解為 : x = M1∙t1∙a1 + M2∙t2∙a2 + M3∙t3∙a3
    • 把x mod M 得到唯一解

---------------

小結

今天把之前文章中提到的東西整理再一起惹(水了一天w)，不過解的題目還不夠多，經驗還不夠，所以沒有甚麼解題技巧，之後解了學到新東東會再回來更新筆記!

---------------

參考資料

• 模運算 : https://zh.wikipedia.org/zh-tw/%E6%A8%A1%E7%AE%97%E6%95%B8
• 模反元素 : https://zh.wikipedia.org/zh-tw/%E6%A8%A1%E5%8F%8D%E5%85%83%E7%B4%A0
• 利用擴展歐幾里德求模反 : https://www.youtube.com/watch?v=fz1vxq5ts5I&t=41s&ab_channel=EmilyS
• 輾轉相除法 :　https://www.csie.ntu.edu.tw/~b98902112/cpp_and_algo/cpp02/euclidean_algorithm.html
• 擴展歐幾里得算法 : https://zh.wikipedia.org/zh-tw/%E6%89%A9%E5%B1%95%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%97%E7%AE%97%E6%B3%95
• 擴展歐幾里得算法(影片講解) : https://www.youtube.com/watch?v=hB34-GSDT3k&t=2s&ab_channel=GVSUmath
• 費馬小定理 : https://zh.wikipedia.org/zh-tw/%E8%B4%B9%E9%A9%AC%E5%B0%8F%E5%AE%9A%E7%90%86#%E5%8E%86%E5%8F%B2
• [離散數學] 費馬小定理 : https://ithelp.ithome.com.tw/articles/10205906
• 二次剩餘 : https://zh.wikipedia.org/zh-tw/%E4%BA%8C%E6%AC%A1%E5%89%A9%E4%BD%99
• 二次剩餘筆記 : http://gotonsb-numbertheory.blogspot.com/2014/04/quadratic-residues.html
• 勒讓德符號 : https://zh.wikipedia.org/wiki/%E5%8B%92%E8%AE%A9%E5%BE%B7%E7%AC%A6%E5%8F%B7
• 中國剩餘定理 : https://zh.wikipedia.org/zh-tw/%E4%B8%AD%E5%9B%BD%E5%89%A9%E4%BD%99%E5%AE%9A%E7%90%86
• 中國剩餘定理詳細流程模擬 : https://www.mathcelebrity.com/chinese.php