前言

今天來解一題就好，一樣為writeup，這題為中國剩餘定理

Writeup

Chinese Remainder Theorem

題目

網址 : https://cryptohack.org/courses/modular/crt1/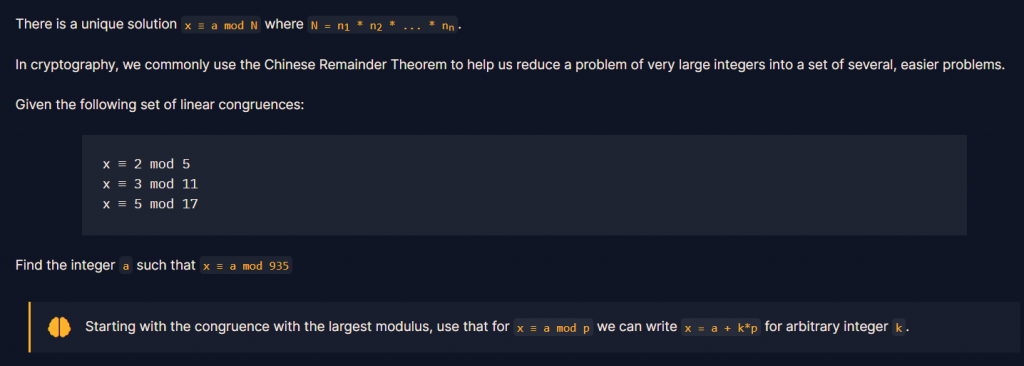

思路

利用中國剩餘定理求通解後，把"解" mod 935 得到x

解法

• 中國剩餘定理
  

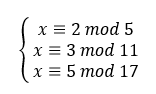
先把M求出來

M = 5 * 11 * 17

再分別算M1, M2, M3

M1 = M // 5, M2 = M // 11, M3 = M // 17

求出M1, M2, M3 分別 mod m1, m2, m3的模反元素

利用t1 = inverse(M1, 5), t2 = inverse(M2, 11), t3 = inverse(M3, 17)

最後可得到通解X = M1∙t1∙a1 + M2∙t2∙a2 + M3∙t3∙a3

最後的最後，把它mod M 得出最小正整數解

X%M

詳細流程模擬可以參考此網址 : https://www.mathcelebrity.com/chinese.php?matrix1=x+%3D+2+mod+5%0D%0Ax+%3D+3+mod+11%0D%0Ax+%3D+5+mod+17&pl=Chinese+Remainder+Theorem

• code

from Crypto.Util.number import *
#x ≡ a mod m
#x ≡ 2 mod 5
#x ≡ 3 mod 11
#x ≡ 5 mod 17
a1, a2, a3 = 2, 3, 5
m1, m2, m3 = 5, 11, 17
M = 5 * 11 * 17
M1, M2, M3 = M // 5, M // 11, M // 17

t1 = inverse(M1, 5)
t2 = inverse(M2, 11)
t3 = inverse(M3, 17)

X = M1*t1*a1 + M2*t2*a2 + M3*t3*a3
print(f"flag : {X % M}")

• output
  

flag : 872

統整

• Chinese remainder theorem 中國剩餘定理
  • 假設整數m1, m2, ... , mn其中任兩數互質，則對任意的整數：a1, a2, ... , an，方程組S有解
    
  • 求通解步驟(在此舉例有3個式子)
    
    • 先求M = m1 * m2 * m3
    • M1 = M//m1, M2 = M//m2, M3 =M//m3

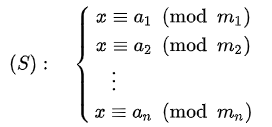
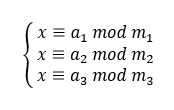
    e.g. a = 5 // 2, a = 2, 由此例子可知" // " 意思為除後取整數商的部分

    • 求M1, M2, M3的模反元素，分別為t1, t2, t3
    • 最後通解為 : x = M1∙t1∙a1 + M2∙t2∙a2 + M3∙t3∙a3
    • 把x mod M 得到唯一解

小結

今天只解這一題，難度比昨天簡單一點，這個課程剩下兩題為類似總複習的，就不會像這樣單一主題(比如這篇主題為中國剩餘定理)，所以就把那兩題放一天，明天預計會先做統整，之後再去解那兩題，最後步入古典密碼!

參考資料

• 中國剩餘定理 : https://zh.wikipedia.org/zh-tw/%E4%B8%AD%E5%9B%BD%E5%89%A9%E4%BD%99%E5%AE%9A%E7%90%86
• 中國剩餘定理詳細流程模擬 : https://www.mathcelebrity.com/chinese.php