圖由vertices(or nodes)和連結nodes間的edges組成。以下是有關圖的一些名詞介紹:

• Vertices (vertex): 圖上的節點
• Edge: 節點間的連結
• Unweighted graph: 圖上的連結完全沒有權重(weight)
• Weighted graph: 圖上任一連結有權重(weight)
• Undirected graph:圖上沒有連結有方向性
• Directed graph: 圖上的連結有方向性
• Cyclic graph: 圖裡至少有一循環(loop)
• Acyclic graph: 圖裡沒有循環(loop)
• Complete graph: 任兩節點都有edge將他們相連
• Tree: directed acyclic graphs的其中一個特別例子。
  Graph 用程式碼表示可以用adjacent matrix, adjacent list 來表示。(如下圖)
  

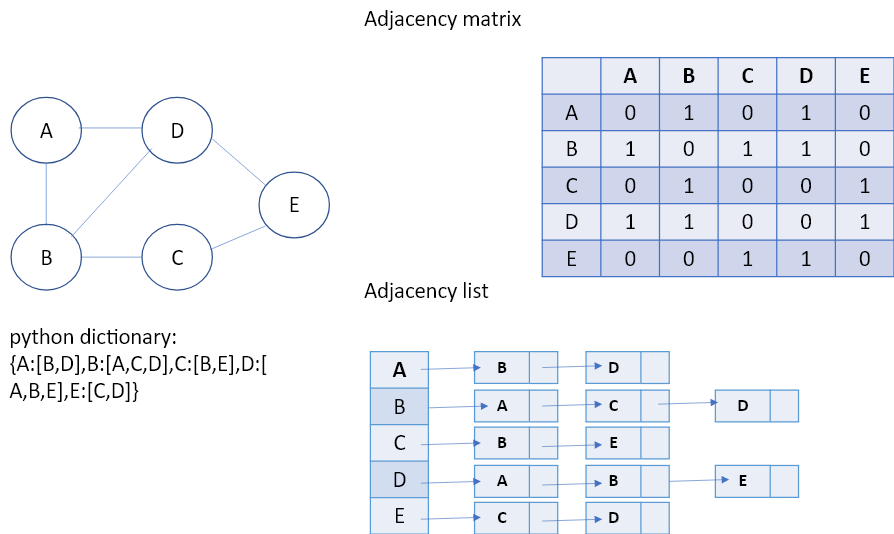
而走訪圖(Traverse graph)的方式可以用 Breadth First Search(BFS， 廣度優先)或是Depth First Search (DFS，深度優先)。在廣度優先的traversal裡，先設定一個起點，然後先拜訪起點鄰近的節點，再拜訪較遠的節點，我們可以用之前學過的Queue來解決這個問題。在深度優先的traversal裡，也是先設定一個起點，然後接續往較遠的節點拜訪，其概念適合用我們之前學過的stack來解決這個問題。下面我們用python來試做一個unweighted graph:

from collections import deque, defaultdict

class graph:
    #這裡我們用defaultdict，所以如果字典裡找不到key，他會見一個key然後value為空白的list
    def __init__(self):
        self.gdict = defaultdict(list)

    def addEdge(self, v1, v2):
        self.gdict[v1].append(v2)
        self.gdict[v2].append(v1)

    def removeEdge(self, v1, v2):
        self.gdict[v1].remove(v2)
        self.gdict[v2].remove(v1)
        if self.gdict[v1] == []:
            self.gdict.pop(v1)
        if self.gdict[v2] == []:
            self.gdict.pop(v2)

    def __str__(self):
        res = ''
        for key, value in self.gdict.items():
            res += f'{key}:{value}\n'
        return res
        
# Breadth First Search: 我們用queue，因其first in first out 的特性
# 因為在最差的情況下(complete graph)每個節點都要每個edge都要visit
# 時間複雜度: O(V+E), 空間複雜度: O(V)
    def BFS(self, start):
        customqueue = deque()
        customqueue.append(start)
        visited = set()
        while customqueue:
            popped_value = customqueue.popleft()
            if popped_value not in visited:
                visited.add(popped_value)
                print(popped_value)
                for i in self.gdict[popped_value]:
                    customqueue.append(i)
# Depth First Search:我們用stack，因其first in last out的特性
# 因為在最差的情況下(complete graph)每個節點都要每個edge都要visit
# 時間複雜度: O(V+E), 空間複雜度: O(V)
    def DFS(self, start):
        customstack = deque()
        customstack.append(start)
        visited = set()
        while customstack:
            popped_value = customstack.pop()
            if popped_value not in visited:
                visited.add(popped_value)
                print(popped_value)
                for i in self.gdict[popped_value]:
                    customstack.append(i)


Example = graph()
Example.addEdge('A', 'B')
Example.addEdge('B', 'C')
Example.addEdge('C', 'E')
Example.addEdge('D', 'E')
Example.addEdge('A', 'D')

print(Example)
print('=== BFS ===')
Example.BFS('A')
print('=== DFS ===')
Example.DFS('A')

>>  A:['B', 'D']
    B:['A', 'C']
    C:['B', 'E']
    D:['E', 'A']
    E:['C', 'D']
    ===BFS===
    A
    B
    D
    C
    E
    === DFS===
    A
    D
    E
    C
    B

本文主要為udemy課程: The Complete Data Structures and Algorithms Course in Python的學習筆記，有興趣的人可以自己上去看看。很多章節的程式碼是根據我自己的理解重新寫過一遍，所以如果覺得跟udemy上課的不太一樣，是正常，你沒有點錯課~~