動態規劃為一解決問題的方法,他將大問題分成小且有重疊的問題,然後將這些小問題的解儲存起來(可以是陣列或者是字典),由此避免重複計算,每當遇到一樣的問題,可以回去搜尋陣列或字典,以此降低時間複雜度。
其中動態規劃的解法可以是top down with memoization (記憶法) 或是 bottom up with tabulation (製表法)。
解決問題的方式是需要透過遞迴來解決子問題,每解決一個子問題,我們透過儲存子問題的結果來避免重複計算。
製表法不使用遞迴,解決完小問題的結果儲存於列表中,基於列表解決剩下的問題。
這裡我們用fibonacci sequence來demo的差別,複習一下fibonacci sequence長這樣:0,1,1,2,3,5,8,13.....(後兩項為前兩項的和)。下面程式碼為當我們想找第N項時,試著用不同的寫法(分冶法、動態規劃的記憶法、製表法):
# 回憶一下,如果是Divide and Conquer(分冶法)
# 把大問題分成小問題以遞迴的方式解決
def Fib(N):
if N in (0,1):
return N
else:
return Fib(N-1)+Fib(N-2)
print(Fib(7))
>> 13
# Dynamic programming: Top Down with memoization (記憶法)
# 這裡可以看到記憶法還是有在用recursion,只是他把前面算過的答案寫在myDict裡,當遇到一樣的問題,可以直接回傳答案(myDict[N))
def Fib(N,myDict):
if N in (0,1):
myDict[N]=N
return myDict[N]
elif N in myDict:
return myDict[N]
else:
myDict[N]=Fib(N-1,myDict)+Fib(N-2,myDict)
return myDict[N]
print(Fib(7,{}))
>> 13
# Dynamic programming: Bottom Up with Tabulation (製表法)
# 這裡我們可以看到他沒有用recursion,而是將所有答案寫成list
def Fib(N):
tb=[0,1]
for i in range(2,N+1):
tb.append(tb[i-1]+tb[i-2])
return tb[N]
print(Fib(7))
>> 13
從上面如果你比較一下分冶法還有動態規劃的時間複雜度會發現,動態規劃比分冶法有效率很多。(分冶法:O(C^n) versus 動態規劃:O(n))
這裡我們把之前分冶法的幾個例子改成動態規劃給大家看看:
給定N,找出用1,3,4三個數表達N的方法數。譬如說N=2,只能是{1,1},回傳1; N=3,可以是{1,1,1}或者是{3},回傳2; N=4,可以是{1,1,1,1},{1,3},{3,1},{4},回傳4,以此類推。
# Divide and Conquer 如果今天是用分冶法:
def NumberFactor(N):
if N in (0,1,2):
return 1
elif N==3:
return 2
else:
op1=NumberFactor(N-1)
op3=NumberFactor(N-3)
op4=NumberFactor(N-4)
return op1+op3+op4
print(NumberFactor(5))
>> 6
# Top Down dynamic programming:
# 這裡可以看到其實top down其實跟分冶法很像,但他把每個階段的答案都存在了字典裡,所以不需要反覆一直計算
def NumberFactor(N,myDict):
if N in (0,1,2):
return 1
elif N==3:
return 2
elif N in myDict.keys():
return myDict[N]
else:
op1=NumberFactor(N-1,myDict)
op3=NumberFactor(N-3,myDict)
op4=NumberFactor(N-4,myDict)
myDict[N]=op1+op3+op4
return myDict[N]
print(NumberFactor(5,{}))
>> 6
# Bottom up dynamic programming:
def NumberFactor(N):
tb=[1,1,1,2]
for i in range(4,N+1):
tb.append(tb[i-1]+tb[i-3]+tb[i-4])
return tb[N]
print(NumberFactor(4))
這裡我們可以感受一下怎麼把昨天的入室盜竊問題改成動態規劃:
# 複習一下分冶法的程式碼,每一步他都可以選要不要偷當下的房子,一旦偷了,他只能從隔壁隔壁的房子開始考慮
def HouseRobber(houses,currentIndex):
if currentIndex>=len(houses):
return 0
else:
steal=houses[currentIndex]+HouseRobber(houses,currentIndex+2)
skip=HouseRobber(houses,currentIndex+1)
return max(steal,skip)
houses=[6,7,1,30,8,2,4]
print(HouseRobber(houses,0))
>> 41
# 動態規劃(記憶法,Top Down),一樣,小問題的答案存在字典裡,你可以看到每次中間的步驟都會去字典找
def HouseRobber(houses,currentIndex,myDict):
if currentIndex>=len(houses):
return 0
elif currentIndex in myDict.keys():
return myDict[currentIndex]
else:
steal=houses[currentIndex]+HouseRobber(houses,currentIndex+2,myDict)
skip=HouseRobber(houses,currentIndex+1,myDict)
myDict[currentIndex]=max(steal,skip)
return myDict[currentIndex]
houses=[6,7,1,30,8,2,4]
print(HouseRobber(houses,0,{}))
>> 41
# 動態規劃(製表法,Bottom up)
def HouseRobber(houses):
tb=[0]*(len(houses)+2)
for i in range(len(houses)-1,-1,-1):
tb[i]=max(houses[i]+tb[i+2],tb[i+1])
return tb[0]
houses=[6,7,1,30,8,2,4]
print(HouseRobber(houses))
有字串s1和s2,試著用插入、取代、刪除等方法,在最少的步驟裡讓s2變成s1。試問最小步驟:
我們回憶一下用divide and conquer寫,你會發現我們其實重複計算了很東西,如圖1: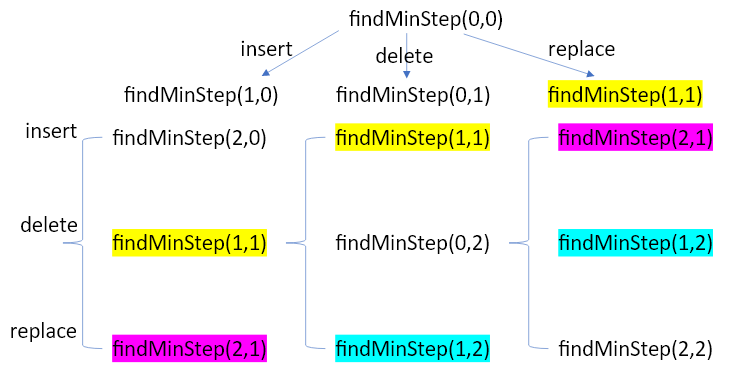
圖1,從圖中可以看到divide and conquer方法在算的時候,標相同顏色者是重複計算的,我們可以試著把它存在array或是dictionary中,改成dynamic programming的方法。
def findMinStep(s1,s2,index1,index2):
if index1==len(s1)-1:
return len(s2)-index2
elif index2==len(s2)-1:
return len(s1)-index1
elif s1[index1]==s2[index2]:
return findMinStep(s1,s2,index1+1,index2+1)
else:
deleteop=1+findMinStep(s1,s2,index1,index2+1)
replaceop=1+findMinStep(s1,s2,index1+1,index2+1)
insertop=1+findMinStep(s1,s2,index1+1,index2)
return min(deleteop,replaceop,insertop)
print(findMinStep("table", "tbrltt",0,0))
Dynamic programming with dictionary
他們核心的概念都一樣,只是把中間值改存在字典裡而已
def findMinOperationBU(s1, s2, tempDict):
for i in range(len(s1)+1):
key='0'+str(i)
tempDict[key]=i
for i in range(len(s2)+1):
key=str(i)+'0'
tempDict[key]=i
for i in range(1,len(s1)+1):
for j in range(1,len(s2)+1):
if s1[i-1]==s2[j-1]:
tempDict[str(i)+str(j)]=tempDict[str(i-1)+str(j-1)]
else:
deleteop=tempDict[str(i-1)+str(j)]
insertop=tempDict[str(i)+str(j-1)]
replaceop=tempDict[str(i-1)+str(j-1)]
tempDict[str(i)+str(j)]=1+min(deleteop,insertop,replaceop)
return tempDict[str(len(s1))+str(len(s2))]
myDict={}
print(findMinOperationBU("table", "tbrltt",myDict))
>> 4
# 可以試著把myDict叫出來看他存了甚麼:
print(myDict)
>> {'00': 0, '01': 1, '02': 2, '03': 3, '04': 4, '05': 5, '10': 1, '20': 2, '30': 3, '40': 4, '50': 5, '60': 6, '11': 0, '12': 1, '13': 2, '14': 3, '15': 4, '16': 5, '21': 1, '22': 1, '23': 2, '24': 3, '25': 4, '26': 5, '31': 2, '32': 1, '33': 2, '34': 3, '35': 4, '36': 5, '41': 3, '42': 2, '43': 2, '44': 2, '45': 3, '46': 4, '51': 4, '52': 3, '53': 3, '54': 3, '55': 3, '56': 4}
Dynamic programming with array
import numpy as np
def findMinOperationBU(s1,s2):
dp=np.zeros((len(s1)+1,len(s2)+1),dtype=int)
for i in range(len(s1)+1):
dp[i][0]=i
for i in range(len(s2)+1):
dp[0][i]=i
for i in range(1,len(s1)+1):
for j in range(1,len(s2)+1):
if s1[i-1]==s2[j-1]:
dp[i][j]=dp[i-1][j-1]
else:
dp[i][j]=1+min(dp[i-1][j],dp[i-1][j-1],dp[i][j-1])
return dp[len(s1)][len(s2)]
print(findMinOperationBU("table", "tbrltt"))
>> 4
# 他出來的array會長這樣,你可對照上面的程式碼看,我們取最後右下角的4
array([[0, 1, 2, 3, 4, 5, 6],
[1, 0, 1, 2, 3, 4, 5],
[2, 1, 1, 2, 3, 4, 5],
[3, 2, 1, 2, 3, 4, 5],
[4, 3, 2, 2, 2, 3, 4],
[5, 4, 3, 3, 3, 3, 4]]
當然LeetCode上還有很多例題,這裡就不再贅述了,感覺這種只能靠多練習才能抓到感覺。
參考資料:
The Complete Data Structures and Algorithms Course in Python (Udemy)
