回溯法(backtracking)是一種用解決問題的演算法，它通常會窮舉不同的可能性，並在達到某條件時回退(backtrack)到達之前的狀態，接著繼續搜索。因為它達到特定條件會退回的特性，它會比單純的窮舉法(brute force)來得快。透過state space tree可能更容易理解: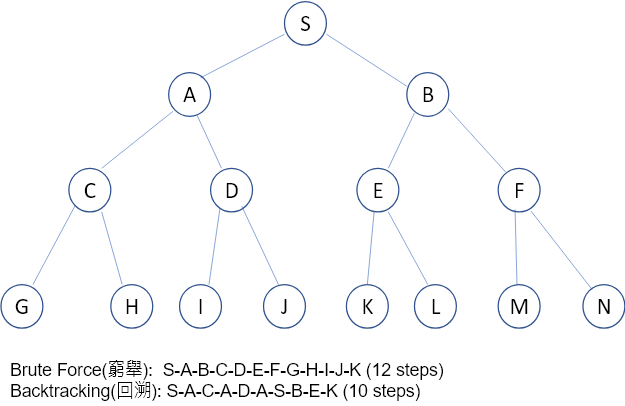

圖1，假使我們今天要從S點到K點，如果是窮舉法需要12步，如果是回溯法只需要10步。

回溯法比較經典的問題應該就是N Queens problem(N個皇后問題):
今天我們要放N個皇后在NxN的棋盤上，為了不使皇后間打架，規則是皇后們1.不能在同一列 2.不能在同一行 3.不能彼此的對角線上。我們直接來看程式碼:

class NQueens:
    def __init__(self,n):
        self.n=n
        self.chess_table=[[0 for i in range(n)] for j in range(n)]
    
    def __str__(self):
        res=''
        for i in range(self.n):
            for j in range(self.n):
                if self.chess_table[i][j]==1:
                    res+=' Q '
                else:
                    res+=' - '
            res+='\n'
        return res
    # 檢查是否可以放queen，回傳True-> safe 可以; False -> 不行
    def is_place_safe(self,row_index,col_index):
        # 檢查同一行
        for i in range(self.n):
            if self.chess_table[row_index][i]==1:
                return False
        # top left to right bottom (左上對角線)
        j=col_index
        for i in range(row_index,-1,-1):
            if i<0:
                break
            if self.chess_table[i][j]==1:
                return False
            j=j-1
        # top right to bottom left (從點到左下)
        j=col_index
        for i in range(row_index,self.n):
            if i<0:
                break
            if self.chess_table[i][j]==1:
                return False
            j=j-1
        return True
    
    def solve(self,col_index):
        # 0,1,2,3 
        if col_index==self.n:
            return True
        
        for row_index in range(self.n):
            if self.is_place_safe(row_index,col_index):
                self.chess_table[row_index][col_index]=1
                if self.solve(col_index+1):
                    return True
                self.chess_table[row_index][col_index]=0
        return False
    
    def solve_NQueens(self):
        if self.solve(0):
            print(self)
        else:
            print('There is no solution for the problem')
         
test=NQueens(4)
test.solve_NQueens()
>>  -  -  Q  -
    Q  -  -  -
    -  -  -  Q
    -  Q  -  -

參考資料:
The Complete Data Structures and Algorithms Course in Python (udemy)