均攤分析練習

今天如昨天最後所說，要再帶一個均攤分析的練習，今天要練習的範例相當經典，而且各大程式語言中像陣列的資料結構均是利用了該分析的結論來實作相關的成員函數。

那麼廢話不多說直接開始我們今天的練習吧！

動態陣列擴充

這邊先用 C++ std::vector::push_back() 簡單介紹一下：

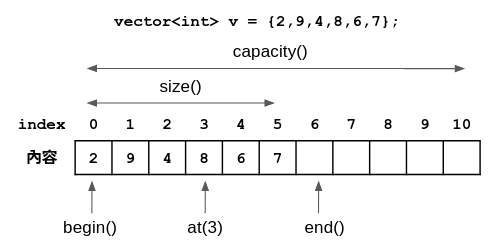
其實 std::vector 有兩種大小：vector::size() 目前能使用的大小、vector::capacity() 在記憶體空間的實際容量

那多出來沒用到的空間要幹嘛呢？C++ 的 vector 中有個常用的成員函式叫作 push_back() ，功能是在 的時間將一個元素插入到陣列的最後面，如果插入時容量有剩就可以直接放；如果容量用完了就重新分配一塊兩倍大的記憶體區塊，並將整個陣列搬過去。聽起來有夠耗時的對吧？不過它的平均操作時間可是 ，我們接下來就是要分析這個 是怎麼來的？

細節可參考 cplusplus.com 的說明；若不熟悉 vector 的可以去 C++ std::vector 用法與範例 先學一下怎麼用再回來看

為了等下方變分析，這邊再較正式地敘述一次問題：
給定一個初始容量為 1 的陣列 arr，該陣列支援函式 push_back() 在陣列後面插入元素；呼叫 push_back() 時若實際空間還有剩，就花費 時間成本直接將放新元素到陣列後面；若陣列可用的容量都已經用完了，假設 表示陣列 arr 當下的容量，則花費就是 的時間成本，此操作會先重新分配一個 大小的記憶體回來，再將 arr 整個複製過去。求這個插入操作的均攤時間複雜度。

記憶體分配在這邊可以暫時先看作 ，因為這個操作在不同系統上皆有不同的行為。而且影響它的變因不單單取決於輸入，還取決於當下空閒記憶體池的量、記憶體碎片化的程度、記憶體管理的演算法等。因此它沒有一個精準的時間複雜度。更深入的討論可以參考： What is the runtime complexity of allocating memory? 、 Time complexity of memory allocation
為此我還在不同平台上實測過記憶體分配的執行時間。使用 Day 4 的測試程式、n 設定到約 大小的 int 陣列 — 大約是 382 MB 左右的連續記憶體、重複次數設定到了一萬的情況下，運行時間也都在 10 「微秒」以下，因此把它當 基本上是沒問題的。

（每次呼叫 push_back() 時間成本的長條圖；from 維基百科）

Aggregate analysis（聚集法）

首先假設我們 push_back() 被呼叫了 n 次，那這樣 push_back() 會分配多少的記憶體給進來的 n 個元素呢？會是 的記憶體。

因此呼叫的 n 次中，有 次 arr 容量會變大；且變大時的時間成本取決於當下的長度加一，不過因為我們是從 1 開始，因此長度必為 2 的冪次。列式來表示總時間就是：

右邊的求和很明顯是等比級數和，因此用等比級數求和公式來分析：

再代回原式：

因此 push_back() n 次的總時間為 ，push_back() 每次的平均操作時間為

The accounting method（記帳法）

假設每次從剛擴充完畢到要再擴充陣列中間間隔為 t 次 push_back()，且此時的長度為 n，則 ，而再度擴充陣列時，複製所花的時間成本正好會是 。

因此我們可以設計預付成本使中間那 次空間足夠時的 push_back() 能為後面擴充的 push_back() 複製時的成本買單，所以預付成本可以設定為 2、再加上本身的實際成本 1，均攤成本等於 3。

均攤成本等於 ，因此平均操作時間為 。

The potential method（位能法）

因為位能分析的重點在讓兩種操作一個出現頻率高並逐步累積位能、另一個操作出現頻率低並會急遽消耗位能，如此一來就能順利求得均攤成本。而在這個問題中所謂的「耗時操作」就是擴充時的 push_back()；「省時操作」就是平常空間夠的 push_back()。

而它們兩者間會對陣列的什麼狀態造成「相反的影響」呢？可以發現到「省時」的 push_back() 會讓陣列的可用空間變大、實際容量不變；而「耗時」的 push_back() 會讓陣列的可用空間變大、實際容量變兩倍。兩者之間的差距就在於實際容量 - 可用空間的量！

因此我們可以試著將位能函數 定義為（目前大小 - 實際容量）。

之所以反過來定義是因為這樣才能造成「耗時」的 push_back() 消耗位能、「省時」的 push_back() 累積位能。

令陣列在 下的目前大小為 、實際容量為 ，

操作	實際成本		均攤成本
不需擴充	1
要擴充

但是 之中的 是會發生的！只要最後的操作是需要擴充的就會發生，但沒關係我們只要額外補上這個數即可，因為最後一個操作可能造成的負位能差會是 。

因為 必定是在最後一個操作前 ，不然最後一個操作不會需要擴充，因此此時的 ，也就是要再 push_back 一個元素的狀態。

因此 n 個操作的總時間複雜度將會是

因此平均操作時間為 。

參考資料

以下是我寫這兩篇均攤分析文章所參考的網路資源，若我有講解不清的部分請自行至下列資源食用：

• Amortized Analysis 介紹 ：影片，建議要學習正規的分析方法先看這部影片
• Algorithm - 平攤分析 Amortized Analysis ：寫的算白話，可以配合上面影片使用
• 淺談均攤分析 - Amortized Analysis ：寫的也算白話，一樣可以配合上面影片使用
• 圖論演算法ch17 — Amortized Analysis ：有提供 pseudo code 超級讚！它最後所說的 Dynamic Tables 應該就是本篇所說的 push_back 的均攤分析，不過它好像多了一個減少記憶體的機制，這邊請留言區大神解答一下這和我上面所分析的動態陣列有什麼不同嗎？
• 算法課筆記系列（七）—— 平攤分析Amortized Analysis ：文章略長，建議有概念後抓重點看就好
• 花花酱 Amortized Analysis 均摊分析 SP7 ：講解上比前面更細，若覺得前面講的分析太理論的話可以參考看看，只是沒有講到位能分析
• 如何理解算法平摊分析中的势能方法（Potential Method）？ ：位能=勢能，這篇的主要價值在於它把位能分析的概念說的很簡單
• 势能分析法 ：專講位能分析，不過它後面的例子都比較進階，請斟酌使用
• 时间复杂度-势能分析浅谈 ：同上，後面的例子較進階，請斟酌使用
• AIdrifter CS 浮生筆錄
  Competitive Programming’s Handbook
  Ch8 Amortized Analysis 平攤分析 ：很棒的整理，例子也不太難，有興趣可以看看
• Amortized analysis平摊分析和Competitve analysis竞争分析的关系 ：講的也很不錯，不過建議抓重點就好
• 动态数组（vector）-详解均摊复杂度分析和避免避免复杂度的震荡（C++实现） ：主要是它有實作，很棒
• 平攤分析(維基百科) ：wiki 對我的主要作用是指引我該往哪學，還有它的示意圖很棒XD

小結

時間複雜度分析技巧的文章到此終於是告一段落了完結撒花！

那麼我們接下來要進入什麼新主題呢？嘿嘿各位明天就知道囉，請各位敬請期待！