前言

在機器學習和深度學習中，優化器就是個能夠優化模型的工具，用梯度下降法幫我們調整模型參數以最小化 ( 優化 ) 模型的損失函數，在訓練過程中，模型根據輸入數據進行預測，然後計算預測結果和實際目標之間的損失並用梯度下降的算法逐漸優化模型參數，以使這個損失函數最小化，從而改進模型的預測能力。

然而在做梯度下降的時候也會遇到一些問題，若損失函數如果存在鞍點和局部最小值，當參數移動到鞍點 ( saddle point ) 或局部最佳解 ( local minima ) 的時候，在兩處參數的斜率都等於 0，此時參數就會原地更新，一直停在原地，始終到不了全局最佳解處 ( global minimum )

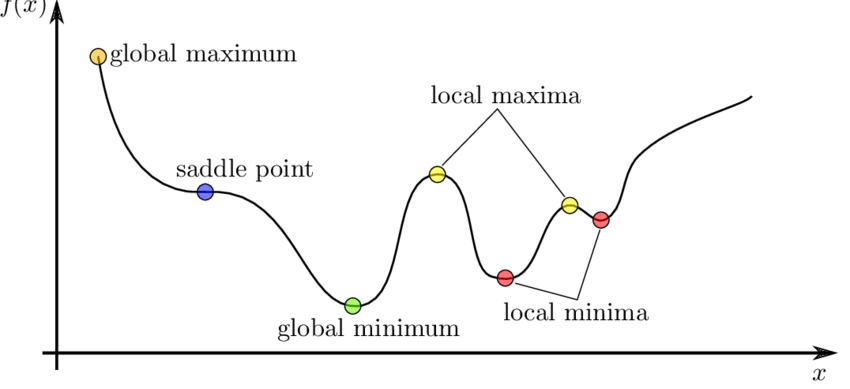
上圖是個單變數的二維地形，你目標是要到達最深的大坑洞 ( global minimum )，但可能到那之前你會先抵達小坑洞 ( local minima )，抵達小坑洞時你看不見後面的大坑洞，依照之前參數更新的算法你會一直深陷停留在當前的小坑洞 ( 參數原地更新 )，就會誤認這個小坑洞就是最深大坑洞 ( 最佳解 )，但其實你根本還沒到大坑洞，最後訓練出來的最佳參數就不是最佳的，關於這個問題，其他的優化器就可以有效地幫我們解決。

各種不同的優化器

參數更新時依據訓練資料的大小，基於梯度下降可區分為三種方法：批量梯度下降 ( BGD )、隨機梯度下降 ( SGD )、小批量梯度下降 ( MBGD )，針對其他目的的優化器常見的有動量法 ( Momemtum )、自適應梯度法 ( AdaGrad )、RMSprop、Adam，今天我們就針對 BGD、SGD、MBGD 來探討。

梯度下降 Gradient Descent

最基本單純的優化算法，參數移動的步長公式：

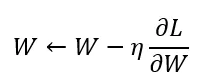
如下圖，梯度下降的目標就是為了最小化損失函數 Cost，以最小化模型預測的誤差，大致步驟：

1. 設定初始參數 ( Initial Weight )
2. 計算出當前參數的梯度 Gradient，多變數函數用偏微分，單變數用微分
3. 依照步長公式參數一步步 ( Incremental Step )往最低點 ( Minimum Cost ) 移動

批量梯度下降 ( Batch Gradient Descent )

基本概念是在每次更新參數時，會使用全部的訓練集資料計算梯度，再把所有資料的梯度都平均起來計算參數的步長做參數更新，下面為每個 epoch 執行的步驟：

1. 對於每個訓練樣本，算出其在損失函數上的梯度
2. 將所有樣本的梯度相加，得到整個訓練數據集的平均梯度
3. 根據所有樣本的平均梯度更新模型參數

優點

• 對於 Convex 的損失函數 ( 凸函數 ) 能夠明確的找到全局最小值 ( 最佳解 )
• 於小資料集上的表現較好
• 每次參數更新時都用全部的資料 ( 每次的樣本都相同 )，因此會更加平滑穩定地收斂

缺點

• 計算成本較高：每次更新參數時都要計算全部訓練集的梯度，導致更新的過程非常緩慢，因此在大資料集上的表現會較差
• 收斂速度慢：在每次更新參數做梯度下降時都用到所有的訓練集資料，可能會導致在尋找最佳解時收斂速度較慢，因為每次更新都需要考慮到所有的資料點，遇到 Non-Convex 的損失函數可能會陷入局部最小值而導致收斂速度減慢

隨機梯度下降 ( Stachastic Gradient Descent )

基本概念為每次更新參數時，用整個訓練資料集的平均梯度來計算更新方向，根據這個方向進行參數的更新調整，以下為每個 epoch 執行的步驟：

1. 隨機抽取一個訓練樣本，計算其損失函數的梯度
2. 將所有樣本的梯度相加，得到整個訓練數據集的平均梯度
3. 根據參數梯度更新模型參數

隨機梯度下降在每次更新參數時，會從全部訓練資料中隨機抽取出一個樣本以計算梯度，因為每次參數的更新我們只會考慮一個訓練樣本資料，速度上就會比 BGD 好很多，只有一個樣本資料也使其無法在計算上實現向量化，計算速度仍比不上 MBGD。

樣本資料的隨機性可能每次的樣本都不同，( 如下圖 ) 導致參數更新的方向較不穩定 ( fluctuations )，可能會更快地趨於局部極小值。

小批量梯度下降 ( Mini-Batch Gradient Descent )

小批量梯度下降在每次更新參數時，不會和 BGD 一樣使用全部訓練樣本，也不會和 SGD 只用一個隨機樣本，而是使用一部分 ( 一個批次 Batch ) 的訓練樣本來計算梯度，Batch Size 可以自行指定，這可以解決 SGD 樣本隨機性導致參數更新方向不穩定的問題，速度上有向量化的實現所以效率較高，以下為每個 epoch 執行的步驟：

1. 隨機打散訓練資料
2. 將訓練資料分成多個小批次（Batch )
3. 遍歷每個小批次，計算其損失函數的梯度
4. 根據每個批次中樣本的平均梯度更新模型參數

在實際應用中，小批量梯度下降通常最長使用的梯度下降法，在訓練過程中可汲取批量梯度下降和隨機梯度下降的優點，達到更好的收斂性能，相對地小批次大小的不當選擇也可能會導致收斂速度慢。

比較

結果

下面三張圖可以比較三種方法在更新參數時的過程走勢，發現到 BGD 非常平緩 ( 最左 )，SGD 最起伏不定，受到較多雜訊影響 ( 中 )，MBGD 的起伏程度介於 BGD 與 SGD ( 最右 )

小結

今天我們學到的優化器：

• 批量梯度下降
• 隨機梯度下降
• 小批量梯度下降

今天先介紹完一部份的優化器，明天再為各位帶來其它的優化器像是 Momentum、AdaGrad、RMSprop、Adam，那我們下篇文章見 ~

參考資料

https://www.researchgate.net/figure/Figure-C1-shows-a-general-one-dimensional-nonlinear-function-exhibiting-the-various_fig18_326112578

https://towardsdatascience.com/batch-mini-batch-stochastic-gradient-descent-7a62ecba642a

https://www.geeksforgeeks.org/ml-mini-batch-gradient-descent-with-python/