前言

梯度下降 ( Gradient Descent ) 是一種最優化模型算法，用於調整模型參數以最小化損失函數。它是機器學習和深度學習中最常用的優化方法之一，今天我們就要來好好探討一下梯度下降究竟是何物。

梯度下降 Gradient Descent

我們知道經過優化後的模型能夠找到一個最能夠接近真實結果的函數用來表示預測結果，那何謂最佳的模型函數 ? 就是其對應的損失函數值會最小，那要如何找到損失函數的最小值，就要歸結到數學問題，即是對某個代表模型損失的損失函數求極值 ( 全局最佳解 )。

假設現在模型的損失函數為 ，可以把損失函數的導函數 ( 橘 ) 和函數本身 ( 藍 ) 畫出來如下二圖 ( 兩圖曲線相同 ) :

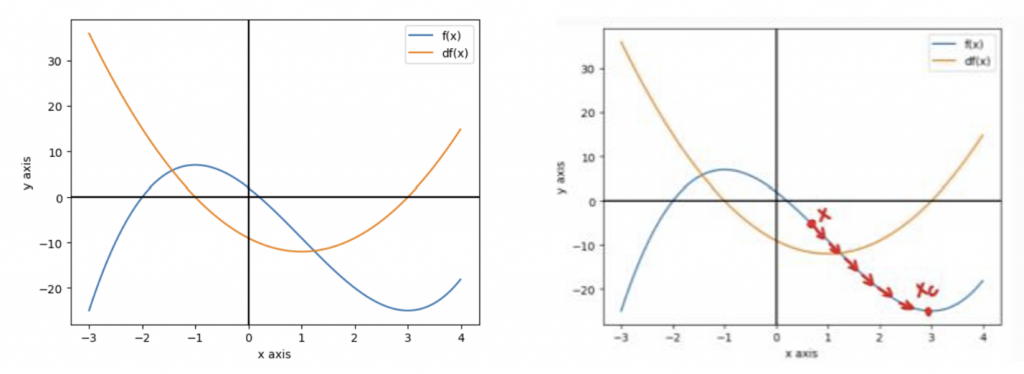
圖中可以找出當 時所對應的 ，代表 在 時為最大或最小，然而一個好的模型它的損失要盡可能最小，因此當 且 為最小值時，此時的 就是最佳解，那要怎麼找到那個 呢 ? 我們就先找一個起始點 ( 模型參數 weight )，如上圖右 就會在函數上一步步移動到最低點 ( 最佳解 ) ( 如上圖右 )，這個過程會不斷地更新模型參數。

而這 每一步移動的變化率為 ，也就是 參數的步長 ( step size )，把當前的 加上 就會得到更新後的 ，也就是下一步要 要移動到的地方，經過一次次的迭代參數更新， 就會一步步地移動並形成一條通往最低點的路徑，這個過程就稱為梯度下降。

單變數損失函數

假設現在模型的參數只有一個有 ( 單變數 )，要求出最佳的 參數，就會用到梯度下降的方法，要實踐這個方法我們只需要用到我們的損失函數 Loss Function ，只要 Loss Function 是可微分的，Gradient Descent 就有辦法求出比較好的參數。

1. 我們一開始可以先隨機找一個初始值
2. 再去計算 在 上的微分 ( 單變數函數斜率 )

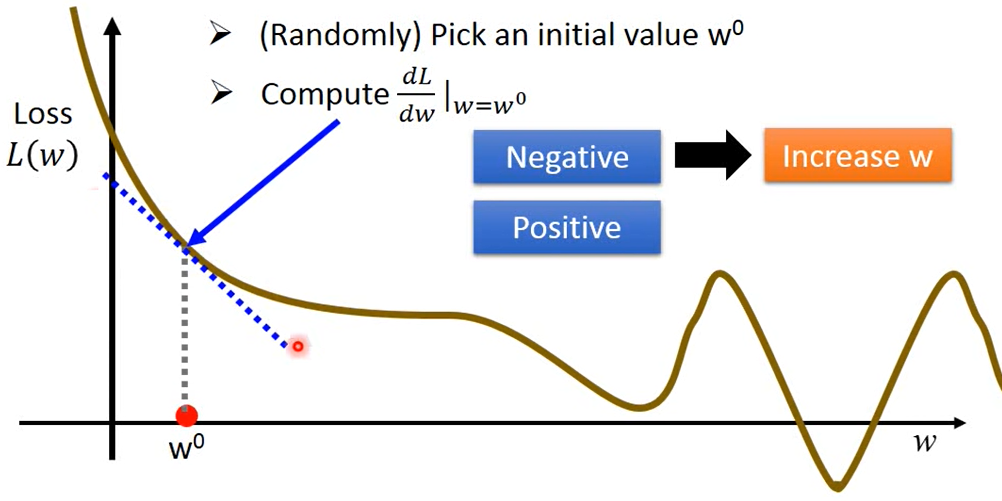
3. 當 < 0 時，在該點的斜率為負，由此可知該點右邊的 一定會比較低，為了要找到比較低的 ，所以該點就往右移動，反之當當該點斜率 > 0 時，該點就要往左移動

4. 那要移動多少呢， 就是參數每步移動的變化率，其取決於 在當前該點 ( ) 上的微分值 :

   

   上面公式可以知道微分值越大，表示 越陡峭，這邊有一個移動的幅度 ，當微分值為負時， 要為正 ( 往右增加 )，微分值為正時 要為負 ( 往左減少 )，因此 前面要加一個負號，也就是 移動的下一步會受負斜率的影響，假設 下一步要移動到 ， 就等於 ，也就是下面參數更新的步長公式 ( → )

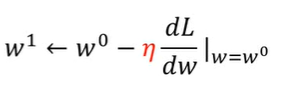
又稱為學習率 ( Learning Rate )，在這邊目的是為了讓移動幅度不僅僅只取決於微分值，它可以是一個預先定好的常數，只要其值越大，移動就越大，學習的效率速度就越高

5. 如此一來參數 就會在一直往左 / 右移動的過程中不斷地更新參數，那這個過程要持續多久，持續到 = 0 時，即到達極小值的地方，而此時因為微分值為零，代入 移動幅度為 0， 就會停止更新參數停在原地，此時的 值所對應的 就是 Loss Function 中最小值，也就是我們要找的最佳 參數
6. 值得注意的是上面那張圖在 一直向右移動時先碰到微分為 0 的地方並不是全局最小值而是局部最小值，但不用擔心，因為在之後線性回歸 ( Linear Regression ) 中的 Loss Function 都會是 convex ( 凸函數 ) 且只要碰到微分為 0 的地方就一定是全局最小值

多變數損失函數

假使現在要訓練的模型參數有兩個 和 ，損失函數即為多變數函數 如下圖，找尋最佳參數的方法就和在單變數損失函數一樣用梯度下降，需要用偏微分的方式計算多變數函數在該點參數上的梯度 ( 求多變數函數斜率 )，藉此讓參數隨著變化率逐步移動。

凸函數 Convex Function

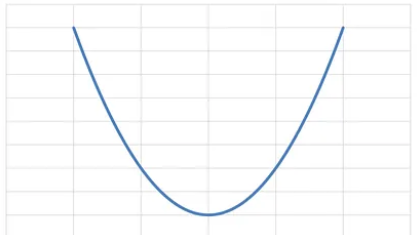
在做梯度下降優化過程中，凸函數和非凸函數是很關鍵的因素，影響了優化的結果，凸函數的局部最小值 ( Local Minimum ) 同時也是全局最小值 ( Global Minimum )，因此模型優化後最終得到的解即是全局最小值

非凸函數 Non-Convex Function

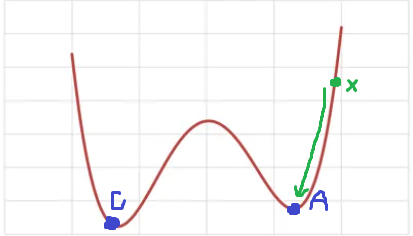
而如果是非凸函數的話，可能存在多個局部最小值，此時做梯度下降時，若 從初始位置朝向最低點移動 ( 如上圖 )，會困陷於局部最小值 ( A 點 ) 而無法找到全局最小值 ( B 點 )，針對此情況使其他種的優化器便能夠解決此問題

總之，凸函數和非凸函數在梯度下降等優化算法中的行為是不同的。凸函數保證梯度下降會收斂到全局最小值，而非凸函數可能會陷入局部最小值。因此，在設計優化算法和選擇初始點時，這些函數的凸性是需要考慮的重要因素。

梯度爆炸和消失

在深度學習梯度下降優化的過程中，會因為存在梯度爆炸 ( Exploding Gradient ) 或梯度消失 ( Vanishing Gradient ) 而難以訓練，在神經網路中，進行反向傳遞時 ( Backward Propagation )，梯度只能一層一層地從最後一層往前傳遞，所謂反向傳遞，就是損失函數對每個參數求導數，因此在有多層的神經網路時，會運用到連鎖率 ( Chain Rule ) 的技巧，反向傳遞過程中梯度會在層層間不斷相乘，此時如果特徵資料間的尺度差異極大，可能會導致計算出的梯度大小極大或極小，此時若梯度不斷乘以絕對值小於 1 的數 ( 梯度極小 )，那麼梯度越接近 0，發生梯度消失，過小的梯度導致參數的更新幾乎停滯，收斂速度極慢，若梯度不斷乘以絕對值大於 1 的數 ( 梯度極大 )，梯度就會越接近無窮而發生梯度爆炸，可能會導致：

• 發散：梯度值變得非常大，參數的更新可能讓模型在每次迭代中越來越遠離收斂的目標，最終使模型的損失值發散至無窮
• 訓練缺乏穩定：梯度爆炸可能導致參數值快速增加，使訓練過程變得不穩定。模型可能會在不同的迭代之間出現大幅度的變化，難以收斂到一個合適的解
• 溢出問題：由於電腦的數值範圍是有限的，梯度值的爆炸可能導致數值溢出，甚至出現 NaN（Not a Number）的情況

因此對資料做標準化，才能夠確保尺度差異不會過大，減少梯度爆炸和消失的情況發生。

小結

今天我們學習到：

• 梯度下降的計算過程
• 凸函數與非凸函數在做梯度下降時的差異
• 梯度爆炸和消失的問題

梯度下降是一種模型的優化方式，也稱做優化器 ( Optimizer )，其實對於不同的問題，我們可以使用不同的優化器，不同的方式來幫助我們優化模型，明天我們就會為各位介紹各種的優化器，那我們就下篇文章見啦 ~

參考資料

https://www.youtube.com/watch?v=fegAeph9UaA&list=PLJV_el3uVTsPy9oCRY30oBPNLCo89yu49&index=4

https://towardsdatascience.com/coding-deep-learning-for-beginners-linear-regression-gradient-descent-fcd5e0fc077d