前言

今天講解三題相關題目，希望大家可以透過這三題更加瞭解遞迴形式的使用方式及時機

UVa 834 - Continued Fractions

題目說明

簡單來說是將一個分數轉換為連分數的形式再輸出

像是題目中給的式子一樣

解題思路

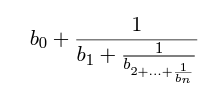
將整數部分先存入陣列，接下來將分子換成原本的分母，分母換成剛剛的餘數，然後不斷重複步驟，直到分子變為零為止，所以依照遞迴的思考邏輯，最重要的中止條件就是分子為零，其他就照著步驟做就可以了

AC Code

#include <bits/stdc++.h>
using namespace std;
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    long long n,m;
    while(cin >> n >> m){
    	vector<long long> ans;
    	while(n % m){
            ans.emplace_back(n / m);
            long long r = n % m;
            n = m,m = r;
    	}
    	ans.emplace_back(n / m);
    	cout << "[" << ans[0] << ";" << ans[1];
    	for(int i = 2;i < ans.size();i++){
            cout << "," << ans[i];
    	}
    	cout << "]\n";
    }
    return 0;
}

UVa 10696 - f91

題目說明

依照題意歸納出式子

解題思路

可以依照此題的題意歸納出的數學式，然後寫成 Top-down 的遞迴式，這樣就可以直接求出解了，程式碼會非常短

AC Code

#include <bits/stdc++.h>
using namespace std;
long long f(long long n){
    if(n <= 100){
        return f(f(n + 11));
    }else{
        return n - 10;
    }
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    long long n;
    while(cin >> n && n){
    	cout << "f91(" << n << ") = " << f(n) << "\n";
    }
    return 0;
}

c547. Bert 爬樓梯

題目說明

簡單來說這是一個爬樓梯問題，可以一次走一階，也可以一次走兩階，然後要詢問爬 階有幾種方式可以走完

解題思路

這其實是一種動態規劃的經典題型，依照題目可以將走幾階分成小問題，因為你要爬 階，可以從 階與 階走 階或是 階，因此可以定義成 ，並且先定義 ，這樣就可以直接得出答案

AC Code

#include <bits/stdc++.h>
using namespace std;
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    long long stair[10010];
    stair[0] = 0,stair[1] = 1,stair[2] = 2;
    for(int i = 3;i <= 10000;i++){
    	stair[i] = (stair[i - 1] + stair[i - 2]) % 1000000007;
    }
    long long n;
    while(cin >> n){
    	cout << stair[n] << "\n";
    }
    return 0;
}

總結

這三題有用到 Top-down 也有 Bottom-up，兩種方法都有各自適合的使用時機，因此還是要透過多多練習題目才會知道什麼題目應該要使用什麼方式

預告

明天就是中秋連假第一天了，因此我應該會介紹一些從之前到現在使用過的學習資源或是競賽心得來取代介紹演算法的文章