前面介紹了各式B+tree的變化型態,
但是仍然是Btree的衍生而已,
無法逃脫比較搜尋法的最佳BigO為log(N)。
雖然說log(N)在n的增長上做了很大的優化,
但當N非常大時,仍然必須使用需多時間來做search。
是否有什麼方把可以打破log(N)的魔咒呢?
有,就是俗稱的Hash Function,
hash結構是一個簡單又好又用結構,
雖然有著自己的缺點,如無法範圍查詢,碰撞等問題。
但優點卻是非常明顯的,
可以利用BigO(1)的時間複雜度來查詢到想要目標。
當N非常大時特別有效。
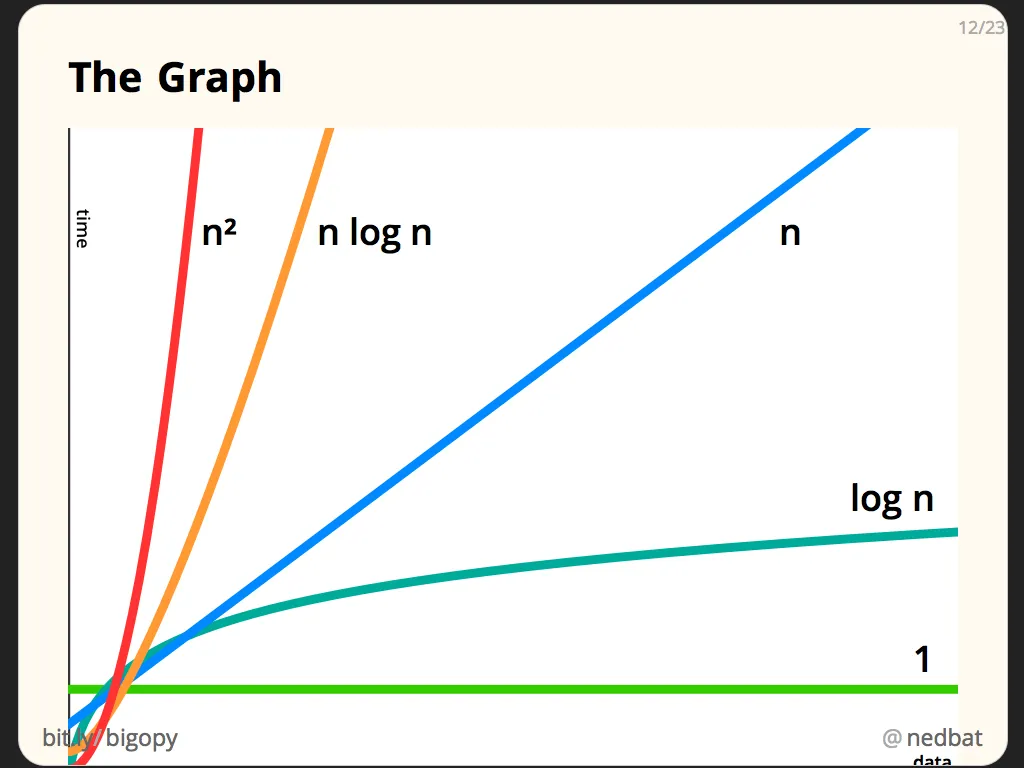
為了突破N增長的瓶頸,可將BigO縮為O(1),
因此我們可以利用這個特性來做衍生。
我們將會先簡單介紹利用hash做index type,
然後介紹hash function應用的衍生bloom filter的原理,
而bloom作為index type會在下一篇做介紹,在這之前,希望大家先完全了解bloom filter的原理。
hash function主要精髓在於經過一個function後,得出數值,
是一個設計原理非常簡單的結構,這裡不做過多基礎的討論,
簡單的介紹如何使用hash index type
(個家db都大同小異,在此使用postgres作為舉例)
CREATE INDEX "{{INDEX_NAME}}" ON "{{TABLE_NAME}}" USING HASH ({{COL_NAME}});
前面理解了hash function是一個設計原理非常簡單的結構,
但就是因為理解簡單,就如同CRUD般的簡單,延伸出了許許多多的眉角,
更是內涵了豐富的知識點,讓事情得到更多優化,也變得並非如此簡單。
Bloom Filter顧名思義就是一種filter,
filter的功能就是做第一層的塞選,把大部分不要的資料過濾掉,
因此Filter將會回傳boolean來表示是否有該筆我們想要的資料
而Bloom filter就是結合hash function概念的衍生filter。
主要有三個角色
插入資料時,利用k個hash function算出來的值,將其對應的bit array由0改成1,
查詢是否有資料時,也利用k個hash function算出來的值,
查看是否其對應的bit array都為1。
主要有三個角色
bloom filter將會使用k個hash function,
這裡的概念有點類似機長與副機長,
機長設定好飛行參數,副機長重新做出雙重驗證。
而k個hash function 就如同有k個副機長。
那麽hash function越多越好嗎?
事情可沒這麼簡單,文章後續會做分析
bit array是bloom filter的特色,
以前我們在學習時做hash function時,
會在資料集之外額外建立一個 array 來儲存資料,該array長度不等於資料集的個數。
hash function會算出該資料所對應的index,然後將值存入該array對應的index。
這裡的bit array和以前學習的不同!!!這裡需要特別注意。
bit array並不是存資料的地方,
而是拿來給hash function 標註如果經過該hash function後這裡有值,
所以如果有k個hash function,那麼也會修改k次bit array。
查找時,如果經過k個hash function後,該k個hash value對應的bit array都為1,表示可能有該值。
反之,諾其中一個為0,表示尚未存過該值。
下圖使用3個hash function與長度為8的bit array做範例
當要[存入]java這筆資料時(上圖2),
經過hash function 1,得出1
經過hash function 2,得出3
經過hash function 3,得出6
然後將這三個bit array的index為1,3,6的位置將0改成1。
當要[查詢]尚未存入的c++這筆資料時(上圖4),
經過hash function 1,得出1,對應bit array為1
經過hash function 2,得出4,對應bit array為0
經過hash function 3,得出7,對應bit array為1
1,0,1並非全為1,因此可以確定該值一定沒有未被存入。
當要[查詢]尚未存入的c++這筆資料時(上圖5),
經過hash function 1,得出1,對應bit array為1
經過hash function 2,得出3,對應bit array為1
經過hash function 3,得出7,對應bit array為1
1,0,1並非全為1,因此可以確定該值可能有被存過。
看完上面的實際演練後,想必大家一定會想說,
什麼叫可能有被存過。
回想一下bloom filter的設計,經過k個hash function,
並將k個bit array的值設定為1,
當越來越多個值被插入,bit array將會越來越滿,變得容易被判定成有被存過。
因此
n筆資料的資料集、k個hash function與長度為m的bit array他們之間的比值會大大的影響誤判率,
這裡我們將分析這個誤判率。
計算誤判率,我們就必須先釐清問題。
回想一下大學時學習的機率與統計中的假設檢定,
Bloom filter
會有 Type 1 Error,偽陽性(false positive),實際上沒有存過,測出有值。
因為bit array太滿了,剛好對應到其他資料所修改過的值。
不會發生Type 2 Error,偽陰性(false negative),實際上有存過,測出沒有值。
因爲只要有插入過值,bit array就會被修改。

知道了Type 1 Error,來看看機率分佈函數,
兩峰為判定正確,為常態分佈,
而FN這個區塊就是我們的Type 1 Error的機率面積。
Type 1 Error,偽陽性(false positive),
實際上沒有存過,測出有值。
主要是因為bit array的值被設定成1,
但該值並非使因為插入該值而生的。
n: 資料集長度
k: hash function個數
m: bit array長度
經過k個hash function後,
某位置沒被選中機率為(1-1/m)^k,
插入n個資料後
某位置沒被選中機率為(1-1/m)^kn
所以將n筆資料全部新增完成後
某位置沒被選中機率為(1-1/m)^kn
某位置被選中機率為1-(1-1/m)^kn
查詢中Type I Error的機率查詢是否有值,所以某位置被選中機率1-(1-1/m)^kn,再做k次方
變成(1-(1-1/m)^kn)^k
看起來有點複雜,來簡化一下,
well-known
得出查詢時命中的機率為
我們得知道Type I Error的機率,
那麼幾個hash function時,誤判機率最小
f(k)=(1-e^(-kn/m))^k
let b=e^(n/m),
簡化
f(k)=[1-b^(-k)]^k
兩邊取對數
ln(f(k))=kln([1-b^(-k)])
我們要取k值的最小,所以希望得到對k做偏微分得0,
f'(k)=0代表極值。
偏微分k
(1/f(k))f'(k)=ln([1-b^(-k)])+[kb^(-k)·lnb]/(1-b^(-k))
而f'(k)=0,所以
0=ln([1-b^(-k)])+[kb^(-k)·lnb]/(1-b^(-k))
移項
ln([1-b^(-k)])= -[kb^(-k)·lnb]/(1-b^(-k))
整理後得
1-b^(-k)=b^(-k)
所以
b^(-k)=1/2
將b帶回e^(n/m)
e^(-kn/m)=1/2
k=ln2·(m/n)
well-known
ln2 ~=0.7
所以
k~=0.7·(m/n)
所以當k為0.7·(m/n)時,會有最低誤判率。
而當k為0.7·(m/n)時,誤判機率為
P(error)
=f(k)=(1-e^(-kn/m))^k
~=0.6158·(m/n)
由上面證明得知,誤判機率與m和n也有著極大的關係
經過上面的解釋,我們可以更近一步地畫出彼此的關係圖

n為資料集的長度,p為誤判機率
可以得知資料集越大,
bit array就會被填得越滿,誤判率會因此提升
m為bit array的長度,p為誤判機率
可以得知bit array越大,
bit array就較不容易被填滿,誤判率會因此降低
k為hash function個數,p為誤判機率
可以得知hash function越多,
每次新增值被填上的bit array就會越多,誤判率會因此提升
而hash function在0.7·(m/n)時,會有最低誤判率。
今天介紹了打破比較搜尋演算法的O(log(n))時間複雜度的限制,就是使用hash function。
並且介紹了hash function的衍生應用bloom filter。
明天將會實際手把手的教學在db中如何使用bloom filter做Index Type。
最後,再來講講bloom filter是如何解決緩存穿透問題。
