今天要來說說「非監督式學習」囉！K-means和KNN真的超常混淆的，尤其在不太熟的時候，就跟路上碰到兩個姓王的陌生人，隔十分鐘再看到你也分不出來誰是老王誰是小王。

但是如果認識之後變成朋友，就很容易認出來啦～

所以努力跟他們變朋友吧！（雖然有點難……

K-means

將資料集分為K個類。

對，就這麼簡單。

如果還記得KNN的朋友，可能會嗷嗷著說：「我記得！這是跟KNN一樣的地方！」

但不對，這是跟KNN不一樣的地方（被毆

監督式學習和非監督式學習分類差別

我們先來看一下這張我從網路上借來的圖片：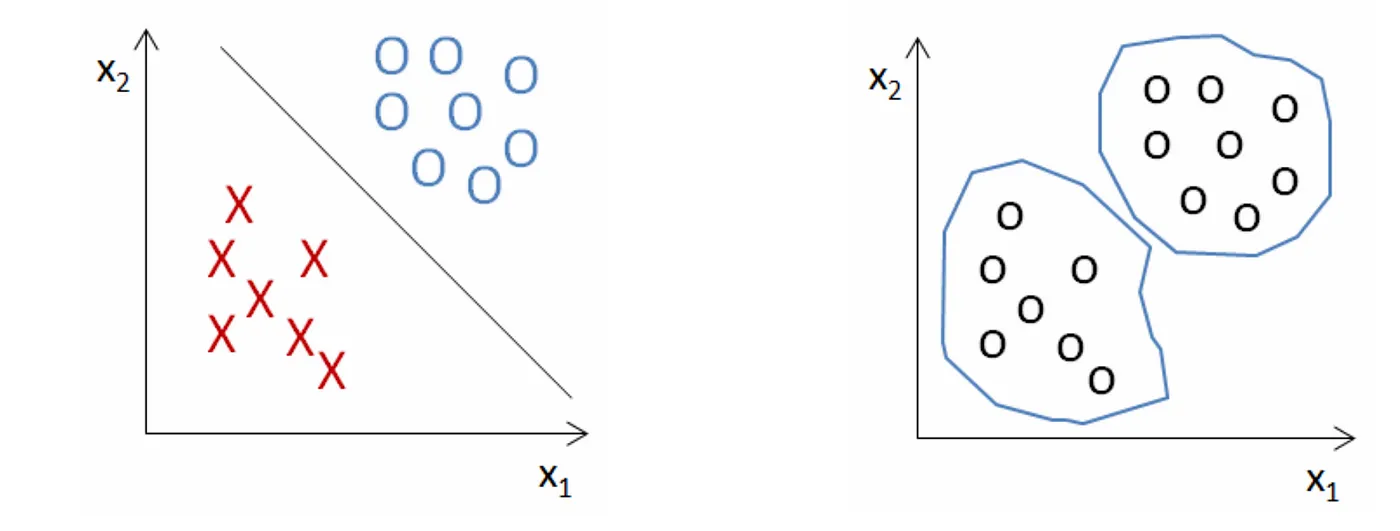

圖片出處：https://medium.com/chung-yi/ml%E5%85%A5%E9%96%80-%E5%8D%81%E5%85%AB-k-means-f92b9f1e8871

從圖片應該可以很清楚看出來，監督式學習因為是已經有答案的狀態，所以純粹是對不同答案的差別做記憶，用來預測：但非監督式學習因為是沒有答案的，所以是一種做出小圈圈的分群。

所以K-means這種非監督式學習，預測結果不會告訴你「答案」（比方說是某個花種），只會告訴你，他們有相同的模式。

K-means怎麼分群？

1. 在資料中加入K個點，設定為「群心」（不是唱歌的那群）。
2. 將資料中的每個點，依照最近的歐幾里得距離，分到最近的群心為一群。
3. 接著，那K個「群心」將會移動，並重新，一直到穩定的分成K個群為止。

單單這樣講，有點抽象，但我看到一個很有趣的比喻，是跟著上面那張圖片的網站一起的。

就想想，當一群學生剛開學進到學校的時候，從不認識到出現小圈圈，每個小圈圈都有一個「頭頭」，這個頭頭就是「群心」。

但畢竟大家都還不熟悉，直到穩定前，這個「頭頭」可能會維持也可能會換掉，同時小圈圈可能會有人走有人進來，直到每個小圈圈都穩定下來為止。

為什麼群心要不斷移動？

我剛開始也有點疑惑，為什麼群心要不斷移動？

雖然說用學校小圈圈的例子理解K-means很方便，但畢竟小圈圈是人組成的，所以會變，不過資料點又不會動。

但其實K-means的方法中，一開始的群心是隨機設定的，所以設定點的位置可能不會是最佳解。等大家都分完群，要重新計算一下中心點，讓群心移過去，但移過去之後發現……

哇。有的點更靠近我，有的點又變成更靠近其他群心了。

所以又要重新分群、計算中心、移動，再視情況重複……聽起來很複雜對吧，幸好這些都是程式跑，不用自己算（汗

結語

基本上這些就是K-means的基本邏輯和運算啦，是不是發現其實也不難理解？

真正難的地方都讓程式包攬去做啦！