上篇文章提到如何透過w跟b的變化查看成本函數，今天我們要找出哪組預測線的w跟b值的成本函數最小，也就是最佳解，因為我們的作法是將w和b的值在一個範圍內把所有的可能都嘗試一遍，最後再找出最佳解，原理相當簡單暴力，所以又叫暴力破解。

首先我們要先寫出一個自定義函數來計算每個填入的w跟b的成本函數，要輸入的四個參數分別是預測線的x, y, w, b，最後會輸出一個叫cost的浮點數，這就是我們要的成本函數

def compute_cost(x, y, w, b):
  y_pred = w*x + b
  cost = (y - y_pred)**2
  cost = cost.sum() / len(x)

  return cost

可以試試看不同值的成本函數是多少

compute_cost(x, y, 0, 0)

再來可以試試當b=0時w輸入不同值的成本函數是多少，我們會建立一個字典costs來記錄輸出的成本函數

costs = []
for w in range(-100, 101):
  cost = compute_cost(x, y, w, 0)
  costs.append(cost)
costs

當然也可以用圖片的方式印出來

plt.plot(range(-100, 101), costs)
plt.show()

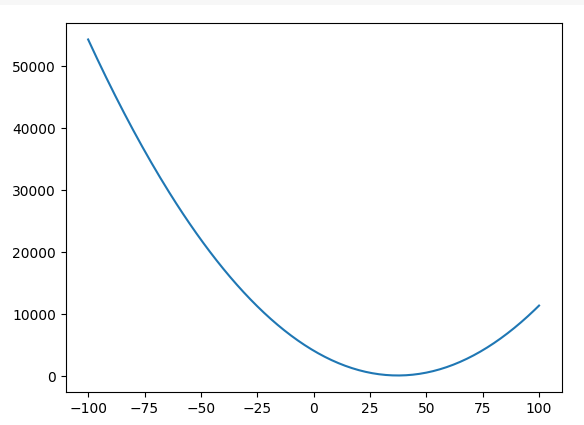
最後就可以將w跟b的值都輸入一個範圍，在寫一個迴圈使兩個值持續遞增來看看最佳的預測線在哪了。因為這個迴圈要跑好幾萬次，等個一段時間是很正常的

ws = np.arange(-100, 101)
bs = np.arange(-100, 101)
costs = np.zeros((201, 201))

i = 0
for w in ws:
  j = 0
  for b in bs:
    cost = compute_cost(x, y, w, b)
    costs[i, j] = cost
    j = j + 1
  i = i + 1

costs

我們以圖片的方式來看看出來的結果吧

plt.figure(figsize=(10, 10))
ax = plt.axes(projection="3d")
ax.view_init(0, 0)
b_grid, w_grid = np.meshgrid(ws, bs)
ax.plot_surface(w_grid, b_grid, costs, cmap="Spectral_r", alpha=0.7)
ax.plot_wireframe(w_grid, b_grid, costs, color="black", alpha=0.1)
ax.set_title("w_cost & b_cost")
ax.set_xlabel("w")
ax.set_ylabel("b")
ax.set_zlabel("cost")
plt.show()

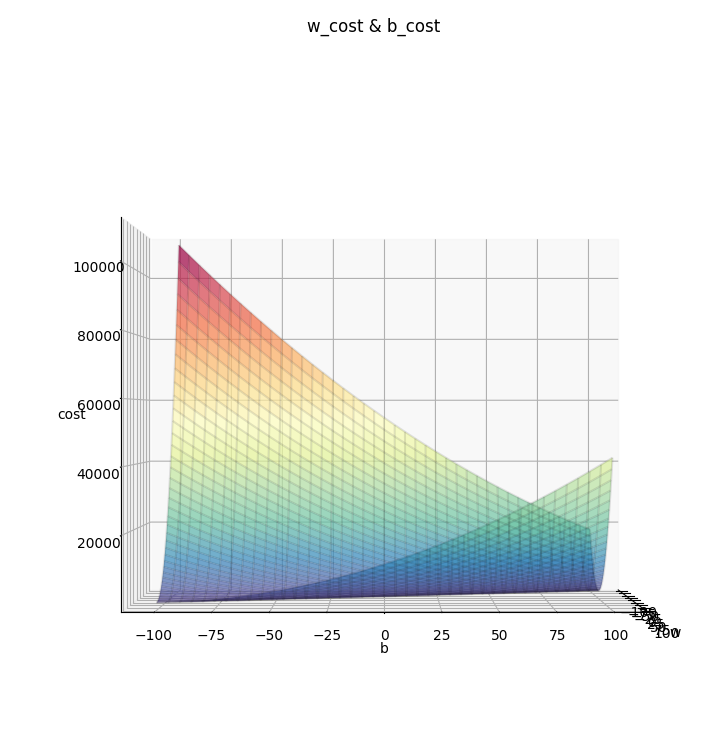
最後我們可以利用這個圖表在電腦中找出最低點，在印出圖片的程式碼中間再加上這幾行就可以了

w_index, b_index = np.where(costs == np.min(costs))
ax.scatter(ws[w_index], bs[b_index], costs[w_index, b_index], color="red")
print(f"當w={ws[w_index]}, b={bs[b_index]} 會有最小cost:{costs[w_index, b_index]}")

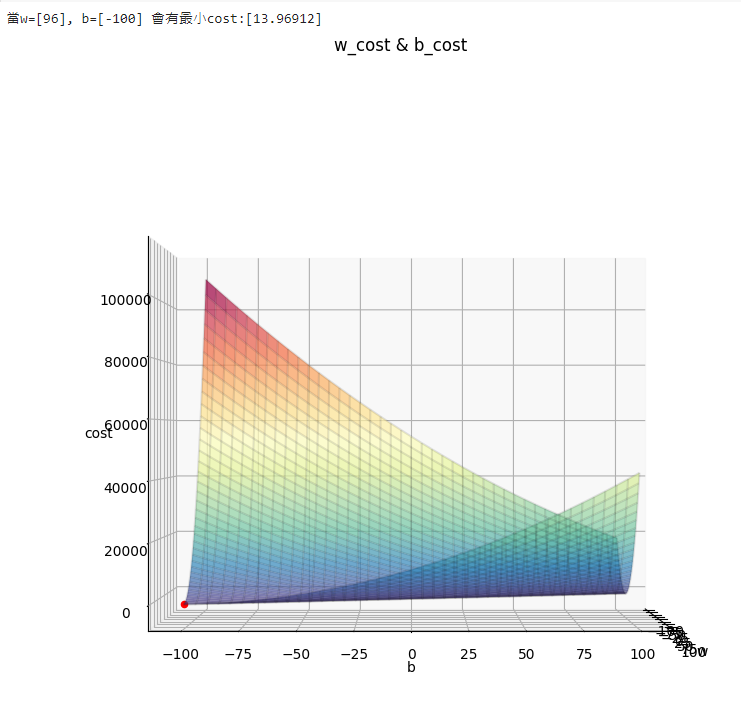
可以得到我們模型最佳預測線中的w=96、b=-100，再將這兩個數字和身高輸入進模型就可以計算出最佳體重了，可以寫一個函數來表示，參數輸入身高及輸出體重，如下:

def Salary_pred(height):
  return (f"身高{height}公尺，理想體重為{96*height - 100:.1f}kg")
Salary_pred(1.7)

就可以得到身高為1.7公尺的人的最佳體重了