Day 6 - 猜猜你幾歲 - 迴歸分析

猜猜你幾歲

網路上有很多能依據照片偵測年齡的人工智慧，這些人工智慧就是應用了迴歸分析。

迴歸分析

迴歸分析的目的是找出多個單一變數和相依變數之間的關係。其中，多個單一變數就是特徵，而相依變數就是預測目標。因此，迴歸分析基本上是一種監督式學習，其目標是找出一個函數y=f(x)。特別地，當f(x)是線性函數時，即它不包含次方項時，就稱為線性迴歸 (Linear Regression)。

迴歸分析問題

適用迴歸分析的問題包括：

1. 時間序列預測：給予過去一段時間的資料，用來預測未來某個時間點的資料，例如氣溫預測。
2. 變數關係預測：給予一些觀察的資料值，來預測另一個變數的值，例如年齡預測。

參數化表示法

假設只有一個變量時，其在平面空間上的圖形就是一條線，橫軸為輸入x，縱軸為預測的y。這個$h_⊖(x)$就是我們的模型，目標是找出最佳的⊖0和⊖1來讓所有的x都對應到正確的y。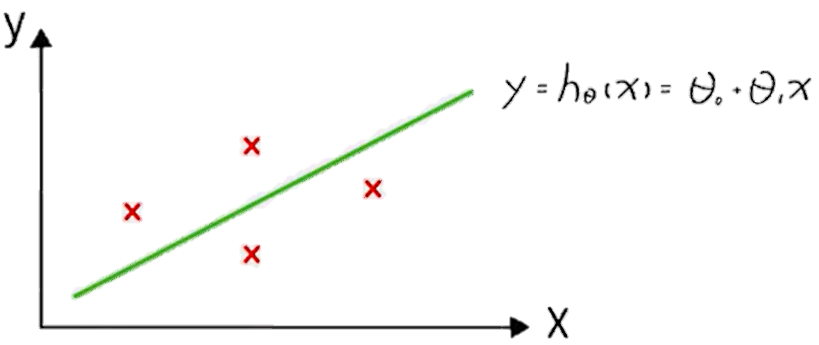

簡單線性迴歸

在只有一個獨立變數和一個相依變數的情況下，稱為簡單線性迴歸。處理這種問題的方法之一是最小平方法，其公式可根據x和y得到⊖0和⊖1。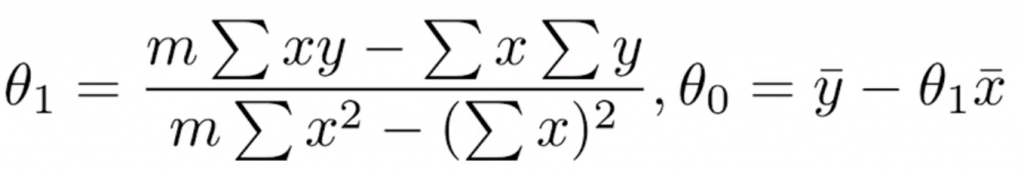

這種方法有一個缺點，當資料集很大時⊖0和⊖1很難求，因此有另一種方法稱為逼近法。

逼近法

目標是求參數⊖，不同的⊖對於輸入的樣本會有不同的輸出估計值。如果有一些訓練樣本，其輸入為x，輸出為y，標記為x1,y1,x2,y2等等。

給定任何一個隨機的參數 ⊖，會得到一個預測的ŷ，這個值和真實值會有差距，稱為預測誤差。把所有樣本的真實值和估計值的差距加起來，得到一個數字J。目標是讓這個誤差J(⊖) 最小，而讓其最小化的方法之一是梯度下降法。梯度下降法較複雜，因此會在之後特別介紹。

多變量的迴歸分析

多變量的迴歸分析是採用多個特徵。

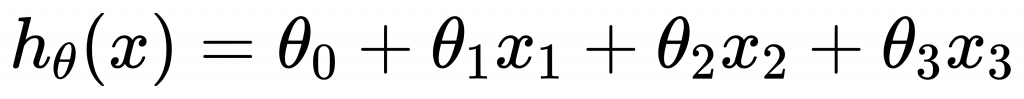
這個方程式仍然是線性的，因此可以用逼近法來計算。

多項式迴歸

現實中很多問題並非線性迴歸，有時需要多項式模型：

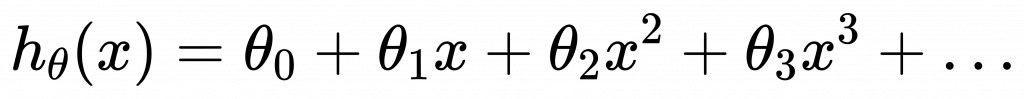
這問題可以轉換成線性迴歸問題。只需進行變數代換，最後的學習演算法也是相同的，可以使用梯度下降法求得⊖的組合。

令x_1=x,x_2=x^2,x_3=x^3，則：

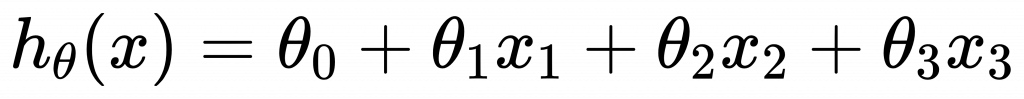
只要把輸入值做平方、三次方、四次方等變換，就能使用線性迴歸模型來解決。