上一次我們提過用來衡量runtime和memoryusage的衡量方法，時間複雜度(Time Complexity)&空間複雜度(Space Complexity)的併用之下，得到的程式不僅是對的而且是有效率的(Efficient)，而我們更希望能達成的是在Inputsize大幅成長之下，程式的scalability性能非常好，也就是runtime只有小小的增加。

以DAY1中我們提到的marriage matching problem為例子，男生三人女生三人之下，我們的Input Size(N)=3^2，我們透過時間複雜度可以知道runtime會和N呈現方程的關係。

假設一個演算法，給定input size 為N，running time 的上限為cN^d（c 與d 皆為大於0 的常數），符合此條件的時間複雜度則稱為多項式時間(Polynomial running time)，符合此條件之下稱為高效率。而當d值越小計算時間越短。

1. 漸進上界Asymptotic Upper Bound 大O符號-O

最壞情況之下的衡量方式。

• 定義：一個函數 ( f(n) ) 的漸進上界是另一個函數 ( g(n) )，表示當輸入規模 ( n ) 足夠大時，( f(n) ) 的增長速度不會超過 ( g(n) )。換句話說，( g(n) ) 是 ( f(n) ) 的一個上限。

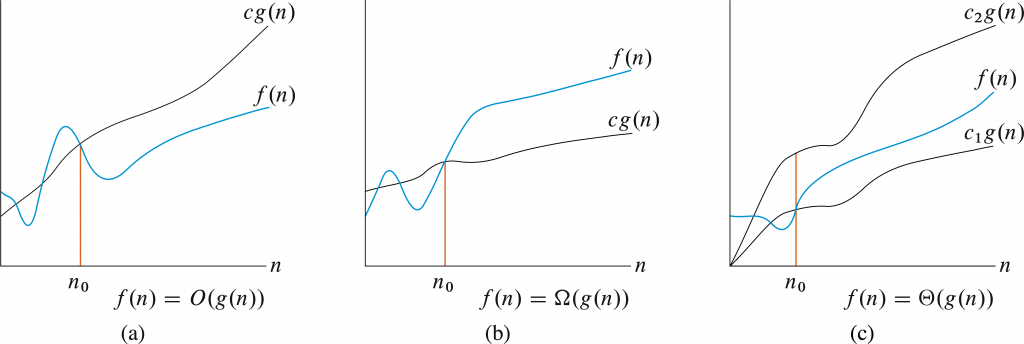
• 數學表示：如果存在正的常數 ( c ) 和 ( n0 )，使得對所有 ( n >= n0 ) 時，( 0 <= f(n) <= c*g(n) )，那麼 ( f(n) = O(g(n)) )。

• 解釋：大O符號提供了算法增長率的最壞情況，給出了時間或空間複雜度的上界。

• 例子：如果一個算法的運行時間是 ( f(n) = 3n^2 + 2n + 1 )，那麼它的大O表示法是 ( O(n^2) )，這意味著當 ( n ) 足夠大時，運行時間的增長速度不會超過 ( n^2 )。

2. 漸進下界Asymptotic Lower Bound 大Ω符號-Ω

最好情況之下的衡量方式。

• 定義：一個函數 ( f(n) ) 的漸進下界是另一個函數 ( g(n) )，表示當輸入規模 ( n ) 足夠大時，( f(n) ) 的增長速度不會低於 ( g(n) )。換句話說，( g(n) ) 是 ( f(n) ) 的一個下限。

• 數學表示：如果存在正的常數 ( c ) 和 ( n0 )，使得對所有 ( n <= n_0 ) 時，( 0 <= c*g(n) <= f(n) )，那麼 ( f(n) = Ω(g(n)) )。

• 解釋：大Ω符號提供了算法增長率的最好情況，給出了時間或空間複雜度的下界。

• 例子：如果一個算法的運行時間是 ( f(n) = 3n^2 + 2n + 1 )，那麼它的大Ω表示法是 ( Ω(n^2) )，這意味著當 ( n ) 足夠大時，運行時間的增長速度不會低於 ( n^2 )。

3. 漸進緊界Asymptotic Tight Bound 大Θ符號-Θ

精確情況下的衡量方式。

• 定義：一個函數 ( f(n) ) 的漸進緊界是另一個函數 ( g(n) )，表示當輸入規模 ( n ) 足夠大時，( f(n) ) 的增長速度與 ( g(n) ) 一致。也就是說，( g(n) ) 同時是 ( f(n) ) 的上限和下限。

• 數學表示：如果存在正的常數 ( c1 )、( c2 ) 和 ( n0 )，使得對所有 ( n >= n_0 ) 時，( 0 <= c1g(n) <= f(n) <= c2g(n) )，那麼 ( f(n) =Θ(g(n)) )。

• 解釋：大Θ符號提供了算法增長率的精確描述，這意味著時間或空間複雜度的上下界相同。

• 例子：如果一個算法的運行時間是 ( f(n) = 3n^2 + 2n + 1 )，那麼它的大Θ表示法是 ( Θ(n^2) )，表示當 ( n ) 足夠大時，運行時間的增長速度正好是 ( n^2 )。

下一個章節開始，我們將要介紹graph演算法，大家期待一下吧！