70. Climbing Stairs

题目描述：

假設你正在爬樓梯，需要爬 n 階才能到達樓頂。每次你可以選擇爬 1 個或 2 個台階。請問有多少種不同的方法可以爬到樓頂？

Example 1:

• Input: n = 2
• Output: 2
• Explanation: 到達頂端有兩種方法：
  1. 1 步 + 1 步
  2. 2 步

Example 2:

• Input: n = 3
• Output: 3
• Explanation: 到達頂端有三種方法：
  1. 1 步 + 1 步 + 1 步
  2. 1 步 + 2 步
  3. 2 步 + 1 步

解題思路:
這道 LeetCode 題目對於第一次接觸的讀者來說可能會有些困難。不過，萬事起頭難，我們可以先透過觀察來找出規律，然後再思考如何解答。

首先，題目已經告訴我們爬到 3 階有三種方法，分別是：

1. 1 步 + 1 步 + 1 步
2. 1 步 + 2 步
3. 2 步 + 1 步

這些方法可以進一步拆解為：

1. 到達 2 階 + 1 步
2. 到達 1 階 + 2 步
3. 到達 2 階 + 1 步

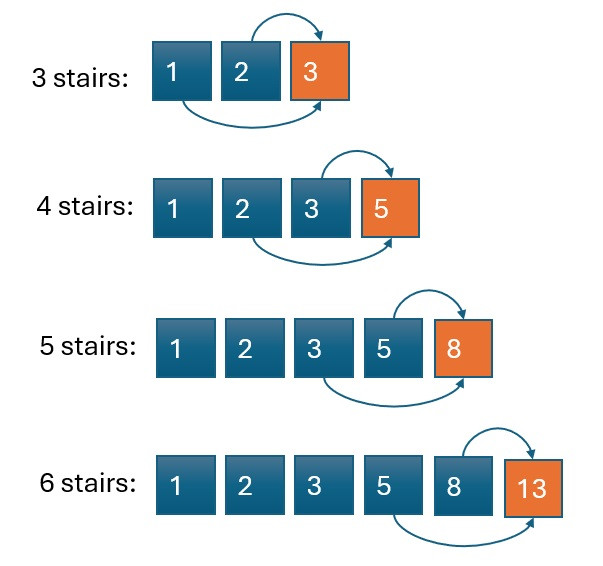
最後，我們可以總結出一個規律：到達 3 階的方法數等於到達 2 階的方法數(2次)加上到達 1 階的方法數(1次)。換句話說，從第 3 階開始，到達某一階的方法數等於前兩階的方法數之和。

以此類推：

• 到達 4 階的方法數為 2 + 3 = 5
• 到達 5 階的方法數為 3 + 5 = 8
• 到達 6 階的方法數為 5 + 8 = 13

這種累加規律讓我們自然聯想到使用動態規劃來解決這個問題。

動態規劃（Dynamic Programming，DP）是一種用來解決複雜問題的方法，通過將問題分解為更簡單的子問題，並將其解答存儲起來以避免重複計算。動態規劃特別適用於那些可以分解為重疊子問題的情況，例如這道爬樓梯的題目。

var climbStairs = function(n) {
    if (n <= 2) return n;

    const dp = Array(n + 1).fill(0);
    dp[1] = 1;
    dp[2] = 2;

    for (let i = 3; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    return dp[n];
};

時間複雜度：O(n)，只需要遍歷一次 n 階樓梯即可計算出所有可能的方法數。
空間複雜度：O(n)，需要額外的陣列來存儲每一階樓梯的方法數。

總結:
這道題目可以歸類為「DP（動態規劃）」。動態規劃在 LeetCode 題庫中占有很大比重，未來我們會遇到許多需要用動態規劃解答的題目。對於剛入門的讀者來說，判斷一個題目是否屬於動態規劃可能會有些困難。這裡提供一個基本的觀察方法：如果題目要求尋找某個最佳解，而這個最佳解只與前面幾次的最佳解相關，那麼這個題目很可能就是 DP 題。一旦判斷出可以使用動態規劃來解題，程式設計往往會變得簡單易行。因此，重點在於觀察題目的規律，判斷它是否屬於動態規劃的範疇，這樣就能順利解決問題。