119. Pascal's Triangle II

题目描述：

給定一個非負整數 rowIndex，返回帕斯卡三角形的第 rowIndex 行。
Example :

• Input: rowIndex = 3
• Output: [1,3,3,1]

解題思路：
這題和上一題 118. Pascal's Triangle 幾乎相同，不過這題只需要回傳某一行的結果，而不需要整個帕斯卡三角形。由於只回傳一行，因此我們可以優化解法，不必使用兩層 for 迴圈來構建整個三角形。

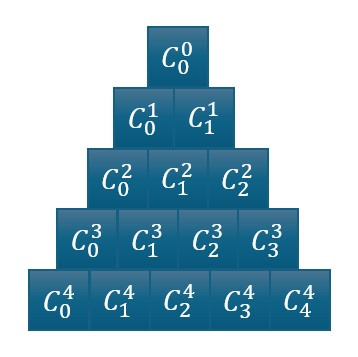
在帕斯卡三角形中，每個數字其實是組合數的一部分。具體來說，第 k 行的第 i 個元素可以用組合數公式表示：

C(k, i) = k! / (i! * (k - i)!)

這個公式代表從 k 個元素中選取 i 個元素的排列組合數。基於這個公式，我們可以不必重新計算所有階乘，而是通過遞推關係直接計算每個元素，遞推公式為：

C(k, i) = C(k, i - 1) * (k - i + 1) / i

這樣可以快速地根據前一個元素計算出下一個元素，並逐步生成一行的所有數字。

var getRow = function(rowIndex) {
    const row = [1];

    for (let i = 1; i <= rowIndex; i++) {
        row.push(row[i - 1] * (rowIndex - i + 1) / i);
    }

    return row;
};

時間複雜度：O(rowIndex)。每次計算下一個元素的時間複雜度為 O(1)，因此總共計算rowIndex個元素。
空間複雜度：O(rowIndex)，用於儲存結果陣列 row。

總結:
這道題目可以歸類為「帕斯卡三角形組合數公式」。透過數學推導，我們可以直接計算組合數來生成帕斯卡三角形的第 k 行，這樣有效減少了不必要的重複計算。相比於之前使用迭代法，這種方法在時間上更加高效，並且保持了最優的空間複雜度。特別是在需要計算較高行數時，這個解法的優勢會更為顯著。

在 LeetCode 的數學題目中，若要找到更優化的解法，通常需要運用數學公式來簡化運算過程，這在像 69. Sqrt(x) 這樣的題目中也是同樣的道理。善用數學推導和公式，可以幫助讀者大幅提升解題效率並更好地理解背後的邏輯。