69. Sqrt(x)

题目描述：

實現 int sqrt(int x) 函數，計算並返回 x 的平方根，其中 x 是非負整數。由於返回類型是整數，結果只保留整數部分，去掉小數部分。

Example 1:

• Input: x = 4
• Output: 2
• Explanation: 4 的平方根是 2，因此返回 2。

Example 2:

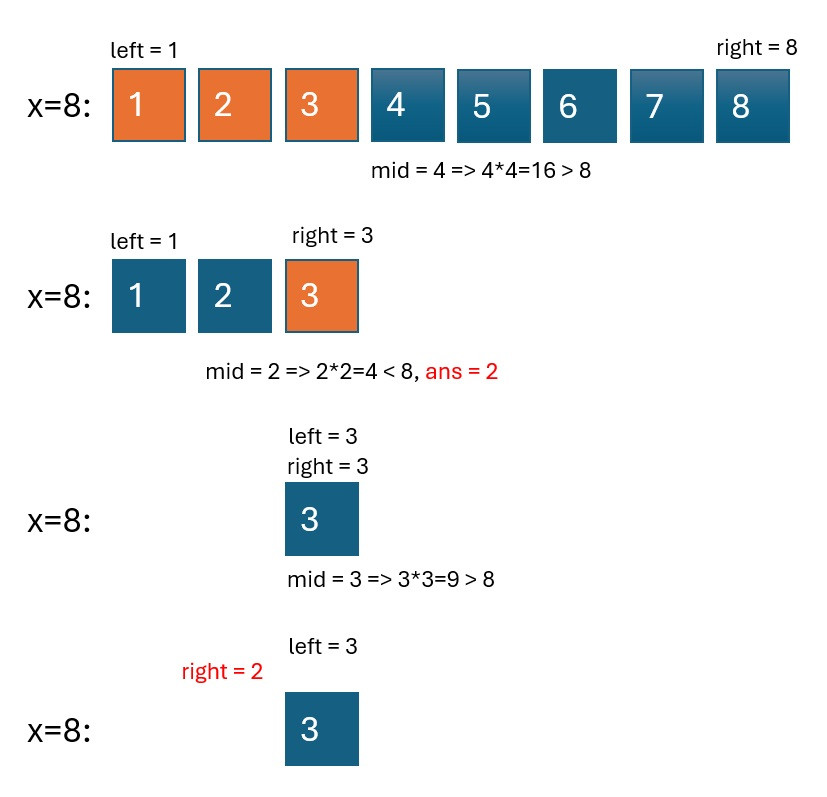
• Input: x = 8
• Output: 2
• Explanation: 8 的平方根是 2.82842...，由於我們只取整數部分，因此返回 2。

解題思路:
這道 LeetCode 題目要求計算 x 的平方根，可以從兩個角度來思考：一個是從軟體工程的角度，另一個是從數學的角度。

首先，從軟體工程的角度來看，我們可以觀察到，求 x 的平方根實際上是在尋找一個滿足條件的數，而這個數會落在 1 到 x 之間。由於這是一個有序的陣列，且對於任何一個非負整數 x，平方根的整數部分是唯一的。基於這些觀察，我們可以使用 Binary Search（二分搜索法） 來解決這個問題，因為它滿足了「排序陣列」和「搜索唯一解」這兩個要素。

在二分搜索法中，我們將 left 設為 1，right 設為 x，然後通過比較中間值 mid 的平方與 x 的大小來尋找 x 的平方根。

具體來說：

1. 如果 mid * mid 等於 x，則 mid 就是平方根，直接返回。
2. 如果 mid * mid 小於 x，說明平方根在右側，因此將 left 更新為 mid + 1，同時將當前的 mid 值保存到 ans 中，因為它是目前找到的最接近的整數平方根。
3. 如果 mid * mid 大於 x，說明平方根在左側，因此將 right 更新為 mid - 1。

當迴圈結束時，ans 的值即為 x 的平方根的整數部分。這樣的方法既保證了搜索的高效性，又確保了結果的正確性。

var mySqrt = function(x) {
    if (x === 0) return 0;

    let left = 1;
    let right = x;
    let ans = 0;

    while (left <= right) {
        let mid = Math.floor((left + right) / 2);
        if (mid * mid === x) {
            return mid;
        } else if (mid * mid < x) {
            left = mid + 1;
            ans = mid;
        } else {
            right = mid - 1;
        }
    }

    return ans;
};

時間複雜度：O(log x)，因為使用了二分搜索法。
空間複雜度：O(1)，只使用了常數級別的額外空間。

從數學的角度來看，求平方根是一個經典問題，其中牛頓迭代法是一種非常適合求解平方根的數值方法。牛頓法的核心是通過迭代逐步逼近方程的根。可以透過圖解來解釋什麼是牛頓迭代法。

首先，在xy軸上畫出一條曲線代表函數f(x)，紅線是函數在某一點 xₙ 的切線，其斜率是導數 f'(xₙ)。斜率的計算公式為：

f`(xₙ) = (f(xₙ) - 0) / (xₙ - xₙ₊₁)

透過推導這個公式，我們可以得出牛頓迭代法公式：

xₙ₊₁ = xₙ - f(xₙ) / f`(xₙ) 

牛頓迭代法表示，下一個 xₙ₊₁ 是通過當前的 xₙ 減去函數值與導數的比值來計算的。這樣，牛頓法逐步接近函數的根，直到達到所需的精度。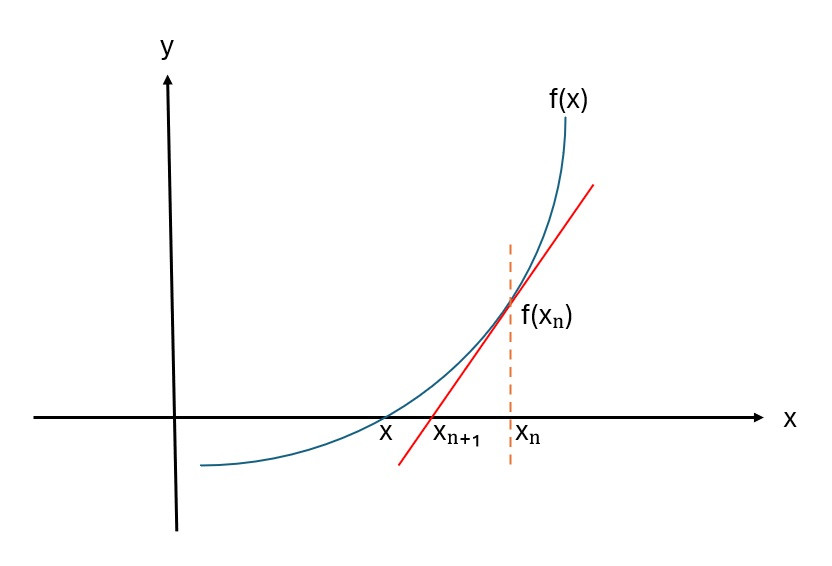

讓我們回到求平方根這個問題。開始先設置函數 f(x) = x² - a，其中 a 是要計算平方根的數。函數的導數為 f'(x) = 2x。將函數和導數代入牛頓法公式，我們得到：

xₙ₊₁ = xₙ - (xₙ² - a) / (2xₙ)

接下來，我們可以將這個計算平方根的迭代公式放入 while 迴圈中，直到當前值和下一個值的差異非常小（小於 1e-7）時，迭代結束，認為已經收斂到結果。否則，將 x 更新為 nextX，繼續迭代。最終返回的結果使用 Math.floor(x)，確保返回的是整數部分，這樣即可得到所求的平方根。

function mySqrt(a) {
    if (a === 0) return 0;

    let x = a;
    while (true) {
        let nextX = x - (x * x - a) / (2 * x);
        if (Math.abs(x - nextX) < 1e-7) {
            break;
        }
        x = nextX;
    }
    return Math.floor(x);
}

時間複雜度：O(log x)，牛頓迭代法的收斂速度非常快，每次迭代大約能減少一半的誤差。
空間複雜度：O(1)，只使用了常數級別的額外空間。

總結:
這道題目可以同時歸類為「二元搜索法」和「牛頓迭代法」。這兩種方法在解決平方根問題上各有優勢，但也有不同的適用場景。

二元搜索法是經典且直觀的解法。它通過不斷縮小搜索範圍，最終找到平方根的整數部分。這種方法易於理解和實現，適合幾乎所有場景，尤其是在資源受限或不需要高精度的情況下。此外，二元搜索法不依賴浮點數運算，因此在如單晶片等需要考慮硬體限制的場景中非常適用。

牛頓迭代法則在效率和精度上表現更為優異。每次迭代都能大幅縮小誤差，收斂速度極快，特別適合處理大數運算。對於需要高精度和快速計算的場合，牛頓迭代法是更理想的選擇。然而，因為它依賴於浮點數運算，這在某些硬體環境下可能會受到限制。

綜合來看，二元搜索法和牛頓迭代法各有千秋。前者適用範圍廣，實現簡單；後者計算更高效但需要浮點數支持。無論是哪種方法，都值得讀者學習，根據具體情況靈活應用，從而更好地解決問題。