104. Maximum Depth of Binary Tree

题目描述：

給定一個二元樹的根節點 root，返回其最大深度。

Example 1: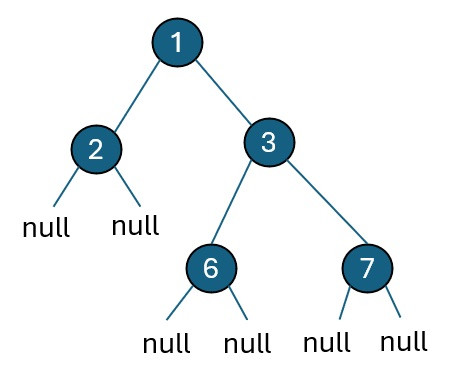

• Input: root = [1,2,3,null,null,6,7]
• Output: 3

解題思路:
這道題目是關於二元樹的實作題，有兩種常見的解法：遞迴法和迭代法。我們先介紹比較直觀的遞迴法來解決這個問題。

遞迴法的思路是將二元樹的最大深度視為其左子樹和右子樹的最大深度中的較大值，再加上根節點所在的那一層，也就是再加 1。具體步驟如下：

1. 檢查節點是否為 null：在遞迴函數中，如果節點為 null，則表示已經遞迴到樹的最底層，回傳層數為 0。

2. 遞迴遍歷左右子樹：如果節點不為 null，則遞迴處理該節點的左子樹和右子樹，分別計算它們的最大深度。

3. 計算最大深度：取左子樹和右子樹的最大深度，然後再加上當前節點所在的這一層，最後回傳這個值。

通過這種方式，遞迴函數會逐層向上返回，最終得到整棵樹的最大深度。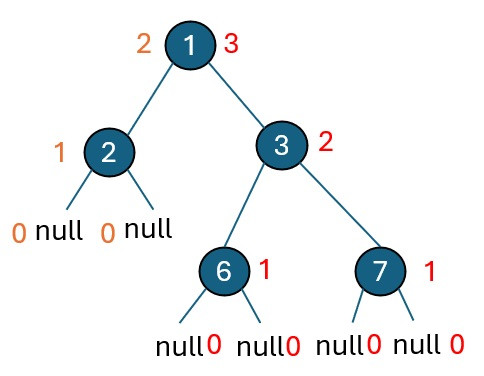

var maxDepth = function(root) {
    if (!root) return 0;

    const leftDepth = maxDepth(root.left);
    const rightDepth = maxDepth(root.right);

    return Math.max(leftDepth, rightDepth) + 1;
};

時間複雜度：O(n)，其中 n 是二元樹中的節點數量。每個節點都會被訪問一次。
空間複雜度：O(h)，其中 h 是樹的高度。遞迴call stack的深度與樹的高度成正比。

迭代法的思路與遞迴法相似，只是將遞迴過程轉換為使用 stack 來進行操作。具體過程如下：

1. 初始檢查：首先，判斷根節點是否為 null。如果是 null，則表示樹是空的，直接返回深度為 0。

2. 初始化 stack：如果根節點不為 null，則將根節點和層數 1 一起 push 到 stack 中。stack 中每個元素包含一個節點以及該節點所處的層數。

3. 遍歷樹的節點：在 while 迴圈中，不斷從 stack 中彈出節點，根據該節點的層數來更新目前的最大層數。

4. 處理子節點：對於每個彈出的節點，將其左子樹和右子樹（如果存在）以及當前層數加 1 一起 push 到 stack 中。

5. 結束迴圈：這個過程會不斷重複，直到 stack 為空。最終，stack 為空時，當前的最大層數即為整棵樹的最大深度。

這種方法通過使用 stack 來模擬遞迴過程，逐層計算樹的深度，並保持跟蹤當前遇到的最大深度。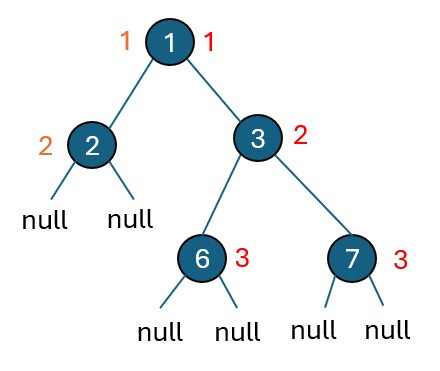

var maxDepth = function(root) {
    if (!root) return 0;

    const stack = [[root, 1]];
    let maxDepth = 0;

    while (stack.length > 0) {
        const [node, depth] = stack.pop();

        if (node) {
            maxDepth = Math.max(maxDepth, depth);
            stack.push([node.left, depth + 1]);
            stack.push([node.right, depth + 1]);
        }
    }

    return maxDepth;
};

時間複雜度：O(n)，其中 n 是二元樹中的節點數量。每個節點都會被訪問一次。
空間複雜度：O(h)，stack 的空間取決於樹的高度。

總結:
這道題目可以歸類為「recursion」和「stack」這兩個分類。透過這道題目可以掌握二元樹的基本操作，並理解如何用遞迴和迭代來解決問題。學習如何計算二元樹的深度，對於處理更複雜的樹狀結構問題將會非常有幫助。這種基礎技能是解決各種樹形結構題目的關鍵，因此建議深入理解和練習。