昨天我們介紹了二元樹的定義和它的種類，今天要來介紹如何走訪所有二元樹的節點

假設一棵二元樹之 root 為 D, 左子樹為 L, 右子樹為 R，則：

1. 前序追蹤 preorder traversal：每棵樹先走訪 D，接著走訪 L 的所有節點，最後走訪 R 的所有節點。
2. 中序追蹤 inorder traversal：每棵樹先走訪 L 的所有節點，接著走訪 D，最後走訪 R 的所有節點。
3. 後序追蹤 postorder traversal：每棵樹先走訪 L 的所有節點，接著走訪 R 的所有節點，最後走訪 D。
4. 層序追蹤 level-order traversal：先走訪第一 level，在走訪第二 level，依序直到走完所有節點為止。

來看個例子：

1. preorder traversal：5 3 2 1 4 6
2. inorder traversal：1 2 3 4 5 6
3. postorder traversal：1 2 4 3 6 5
4. level-order traversal：5 3 6 2 4 1

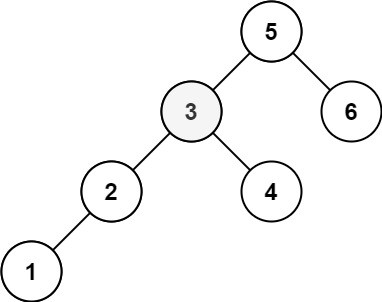
詳細過程：

要注意：是每棵樹都要造著規則來走訪喔

給予追蹤結果決定唯一的二元樹

直接用一個例子來說明：
假設某樹的後序追蹤為：BEFDCA，其中序追蹤為：BAEDFC，是否能決定唯一的二元樹。
答案是可以，因為中序追蹤為 LDR，後序追蹤為 LRD，因此，於後序判斷誰是 D，再去中序中切割左右子樹集合，即可得出唯一的二元樹。
示意圖：

如果是給予前序跟後序呢？

假設某樹的後序追蹤為：CBA，其前序追蹤為：ABC，是否能決定唯一的二元樹。
答案是不一定！
看看下面這張圖：

因為前序跟後序沒辦法切割子樹，當然沒有辦法確定唯一的長相。若前序與後序有 N 個節點互為反序，則 共有 2^(N - 1) 個可能的組合。

traversal 的 code

要用到好久不見的遞迴（Recursion）啦，用 Divided and conquer 的方法來寫 code。
一樣先定義 Node Structure

typedef struct treenode {
    int data;
    struct node* lchild;
    struct node* rchild;
}treenode_t;

1. inorder traversal：先追蹤左子樹，再印出Data，最後追蹤右子樹

void BinaryTree::inorder_traversal(treenode_t* root) {
    if(root == NULL){
        return;
    }else{
        inorder_traversal(root->lchild);
        cout << " " << root->data << " ";
        inorder_traversal(root->rchild);
    }
}

2. postorder traversal：先追蹤左子樹，再追蹤右子樹，最後印出Data

void BinaryTree::postorder_traversal(treenode_t *root) {
   if(root == NULL){
       return;
   }else{
       postorder_traversal(root->lchild);
       postorder_traversal(root->rchild);
       cout << " " << root->data << " ";
   }
}

3. preorder traversal：先印出Data，再追蹤左子樹，最後追蹤右子樹

void BinaryTree::preorder_traversal(treenode_t *root) {
    if(root == NULL){
        return;
    }else{
        cout << " " << root->data << " ";
        preorder_traversal(root->lchild);
        preorder_traversal(root->rchild);
    }
}

4. level-order traversal：要動用到 queue 來幫忙。印出 root 後，將子點 enqueue，接著 dequeue 並印出，並將其子點再 enqueue 進佇列，直到 queue 空。

void BinaryTree::levelorder_traversal(treenode_t *root){
    if(root == nullptr){
        return;
    }else{
        queue<treenode_t*> q;
        q.push(root);
        while(!q.empty()){
            treenode_t* current = q.front();
            q.pop();
            cout << " " << current->data << " ";
            if(current->lchild) q.push(current->lchild);
            if(current->rchild) q.push(current->rchild);
        }
    }
}

而這些程式碼的時間複雜度皆為 O(n) 其中 n 為節點總數，因為是「追蹤」

compiler parsing tree

將我們之前說過的表達式建成 binary tree，使用後序追蹤就可以得到 postfix，前序追蹤就可以得到 prefix。
建立的規則就是：operand 必放樹葉，operator 優先權較高的較接近樹葉，較低的較接近樹根。
例如：infix expression：(4 - 3) * (5 + 6 / 3)
建立compiler parsing tree 並得出 postfix expression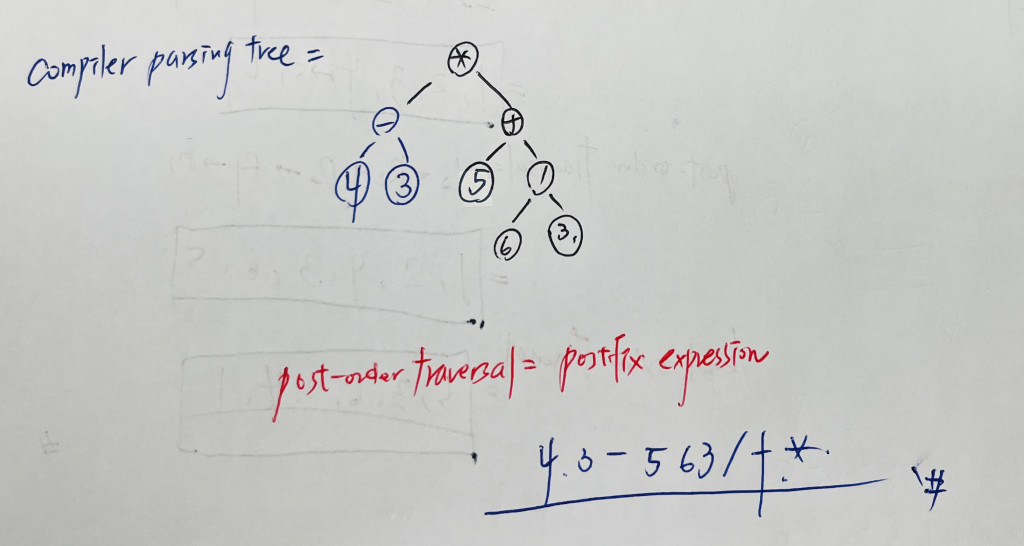

tree sorting

二元樹可以用來進行排序：

1. Binary Search Tree
2. Heap sort

我們明天就要來介紹 Binary Search Tree！