何謂插入排序（Insertion Sort）

插入排序屬於初等排序的其中一種，假設 input 資料共 N 筆存放於 Array[0, 1, ....., (n-1)] 中，則插入排序從 index 1 做到 index (n - 1)，共 N - 1 回合，每回合將 Array[index] 插入前方有 (index - 1)個元素的已經排序之 Array 之正確位置，形成有 index 個已排序之陣列。

Demo

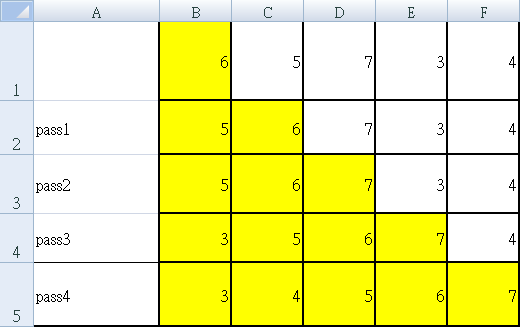
給予：6, 5, 7, 3, 4，(N = 5) 進行 insertion sort：

1. index = 1，將 Array[1] = 6 插入前方 Array[0] 之正確位置：Array = [5, 6, 7, 3, 4]
2. index = 2，將 Array[2] = 7 插入前方 Array[0 ~ 1] 之正確位置：Array = [5, 6, 7, 3, 4]
3. index = 3，將 Array[3] = 3 插入前方 Array[0 ~ 2] 之正確位置：Array = [3, 5, 6, 7, 4]
4. index = 4，將 Array[4] = 4 插入前方 Array[0 ~ 3] 之正確位置：Array = [3, 4, 5, 6, 7]

code

分為 insert(arr, r, i)：arr 為 input data 所在之串列，r 為欲插入之資料，i 則為將 r 插入之 0 ~ i 已排序之串列
接著為 insertSort(arr, n)：arr 為 input data 所在之串列，N 為元素個數。

void insert(int* arr, int r, int i){
    int j = i;
    while(arr[j] > r && j >= 0){
        arr[j + 1] = arr[j];
        j--;
    }
    arr[j + 1] = r; 
}
void insertionSort(int* arr, int n){
    for(int i = 1; i < n; i++){
        insert(arr, arr[i], i - 1);
    }
}

Time Complexity

1. Best case: O(n)
   發生在 input data 由小到大排序時，每次進入排序只需要進行一次比較即可跳出迴圈，因此比較次數共 n - 1 次: O(n)
   遞迴時間函數：T(n) = T(n - 1) + 1。共有 n 筆資料排序時，前面 n - 1 筆使用插入排序，最後一筆僅需 1 次比較。
2. Worst case: O(n^2)
   發生在 input data 由大到小排序時，每次進入排序需要進行 i - 1 次比較才可跳出迴圈，其中 i 為前方串列之元素個數，因此比較次數共 (1 + 2 + 3 + 4 + ...... + (n - 1)) = n(n - 1) / 2 次: O(n^2)
   遞迴時間函數：T(n) = T(n - 1) + (n - 1)。共有 n 筆資料排序時，前面 n - 1 筆使用插入排序，最後一筆需 (n - 1) 次比較。
3. Average case: O(n^2)
   遞迴時間函數：T(n) = T(n - 1) + (n 筆資料時之平均比較次數)。而可能發生之比較為1, 2, 3, ...., (n - 1)比較，因此平均比較次數 = (n(n - 1) / 2) (n - 1) = n / 2 = c * n, c > 0。
   遞迴時間函數修正為 T(n) = T(n - 1) + cn = O(n^2)

Stable sorting method

當 input data 中出現一樣的資料，且順序為 k0, k1, k2, ....
則排序後之結果也保證順序為 k0, k1, k2, ....
因為從 code 來看 k1 並無小於 k0 因此將跳出 while 迴圈，導致其必在 k0 之後