我們曾經做過 WEPL 最小值的計算，透過 Huffman 演算法計算外部節點加權值的最小值
今天介紹的結構，內部節點也有加權值。我們想要求整棵樹的搜尋成本，因此：

search cost = (內部節點加權值 * 該內部節點 level 值)加總 + (外部節點加權值 * (外部節點 level 值 -1))加總

optimal binary search Tree = OBST

optimal binary search Tree 是一個由 N 個 internal nodes 及 N + 1 個 external nodes 所組成的二元搜尋樹，而在 (1/(N+1)) * C(2N, N) 棵不同的二元搜尋樹中，search cost 最小者，則為 OBST

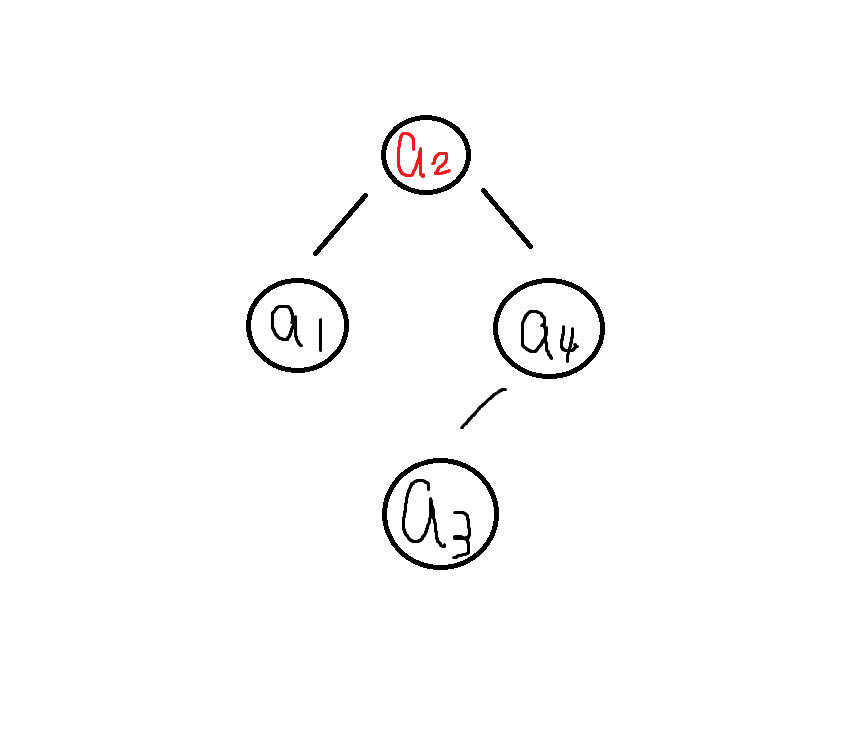
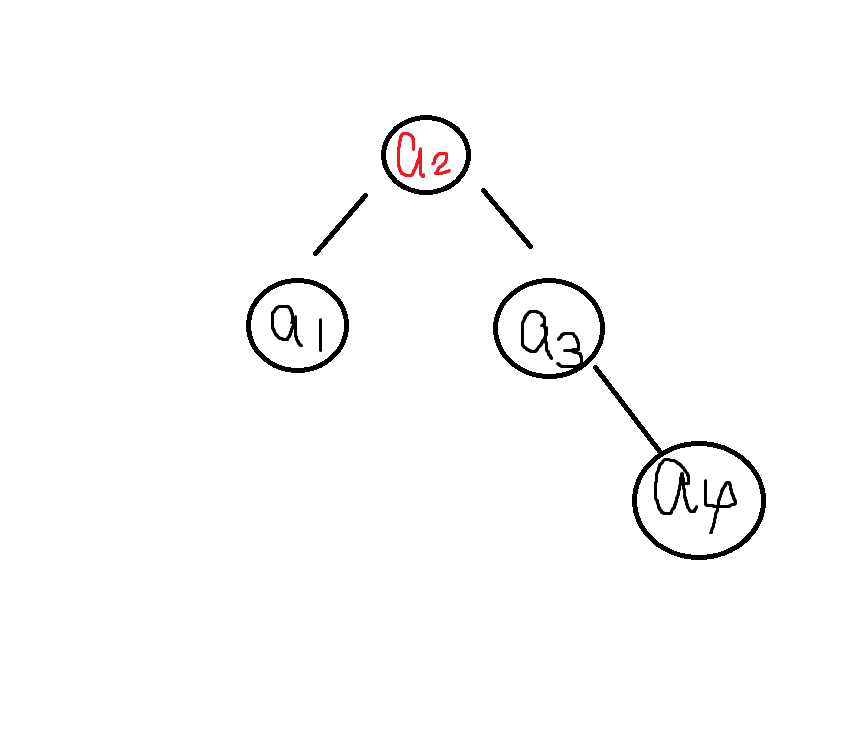
先來看看以下的例子，計算看看 search cost

可以發現，不是高度越高，search cost 越大，因為有加權值的影響

使用 DP 求解 OBST

先來定義一些符號

Ai+1, Ai+2, ......, Aj，代表內部節點，且 Ai+1 < Ai+2 < Ai+3, ...... < Aj
Pi+1, Pi+2, ......, Pj，代表內部節點加權值
Qi, Qi+1, Qi+3, ......, Qj，代表外部節點加權值。因為外部節點比內部節點多一顆，因此從 i 開始標

則令 Tij 為 Ai+1, Ai+2, ......, Aj，所構成的 OBST
若 i = j，代表空樹，不考慮 i > j 的情況

再接著定義符號

Cij 為 Tij 的 search cost
Rij 為 Tij 的 root 編號
Wij 為 Tij 的 內外部節點加權值總和，也就是把所有 Q 值和 P 值加起來

Tii為空樹，因此Cii = 0, Rii = null, Wii = Qi

推算 Cij 公式

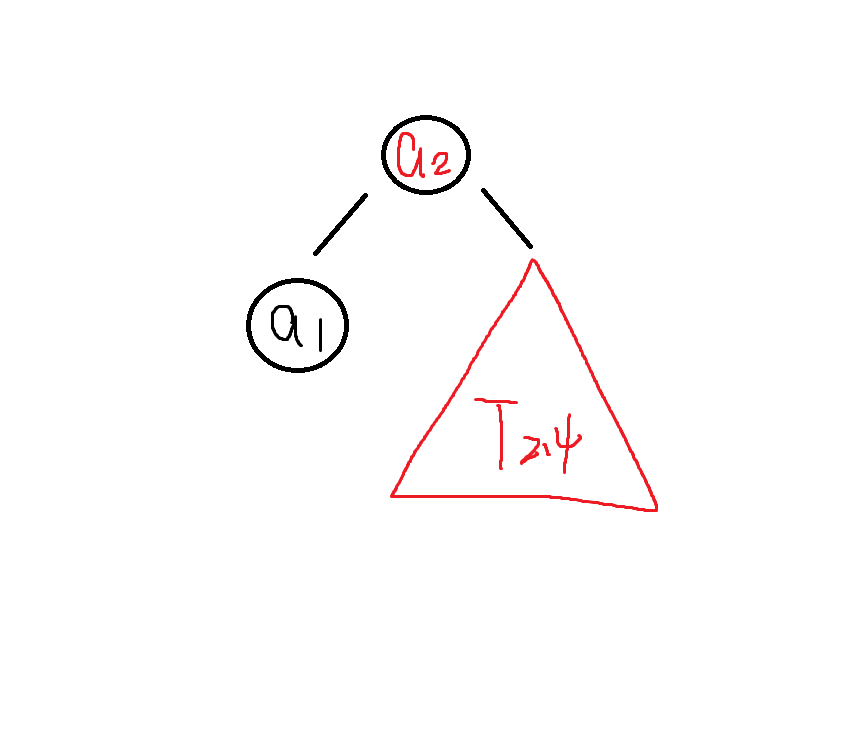
Ai+1, Ai+2, ......, Aj 隨意挑選某 Ak 當作 root 的話，
這棵樹的 Left subtree 為Ti(k-1)，right subtree 為 Tkj

那麼此時 Cij = 1 * Pk + Ci(k-1) + Wi(k-1) + Ckj + Wkj

將 Pk, Wi(k-1), Wkj 相加後，就變成 Cij = Ci(k-1) + Ckj + Wij

為甚麼要加 Wi(k-1) 和 Wkj？

以 Tkj 為例，Tkj 本來是一棵樹，成本是 Ckj，但現在因為 Tkj 變成子樹，意味著所有節點的 level 值都增加 1 了，再根據 search cost 公式，等於是加上所有節點的加權值總和，也就是 Wkj。

認真挑選 root

假設當 Root 的點編號為 R，則 i+1 <= R <= j
Cij = Wij + min{Ci(R-1) + CRj}，把所有可能的 R 看過，找出達成最小值的 Root 編號。

小結

整理到這邊，已經可以確定 OBST 的 Cost 要如何求，接下來只需要靠著 DP 的精神，透過表格來存取每一階段的值，並且逐步找到問題的最佳解，即可找出 OBST

例子

有 4 個 internal node: A1 < A2 < A3 < A4
(P1, P2, P3, P4) = (3, 3, 1, 1)
(Q0, Q1, Q2, Q3, Q4) = (2, 3, 1, 1, 1)
求 Min. search cost 及 OBST 的 Structure

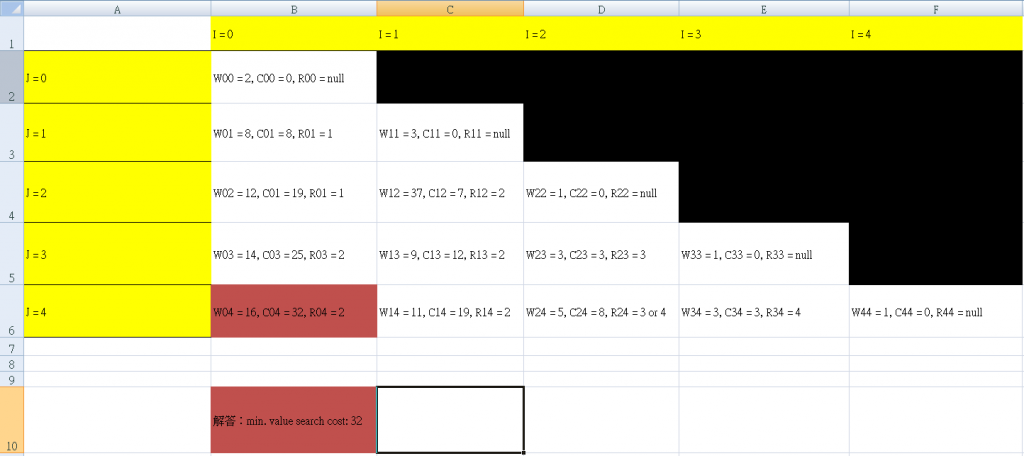
1. 先建立這樣的表，黑色方格為 i > j 的位置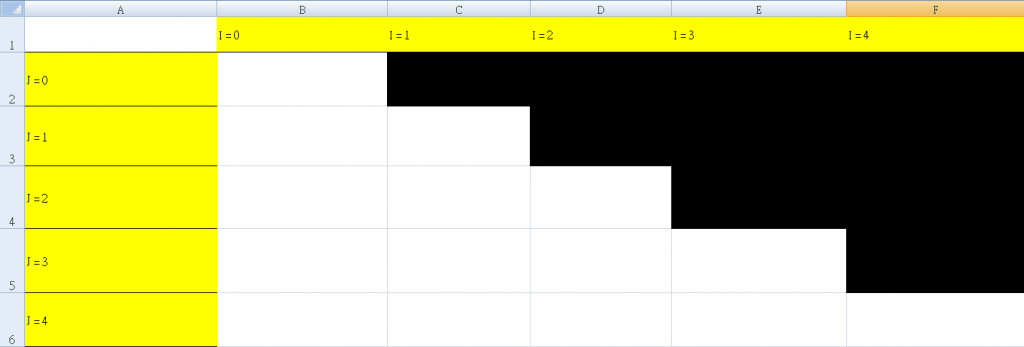
   

2. 接著將空樹的值填上
   

3. 再來就來填 i 與 j 相差 1 的 Tree，因為 i j 相差一，所以 Tij就是由 Aj 所構成的 Tree。
   當然也可以使用 Cij的公式來判斷。
   例如：C01 = W01 + min{Ci(R-1) + CRj}，而 0 + 1 <= R <= 1
   所以 R 只有 1 的選項。將他填入表中。
   

4. 接著填 i 與 j 相差 2 的 Tree，使用 Cij的公式來判斷
   例如：C02 = W02 + min{Ci(R-1) + CRj}，而 0 + 1 <= R <= 2。R 可以選擇 1 或 2
   來比較 C00 + C12 = 7 及 C01 + C22 = 8，因此選擇 C00 + C12 = 7，也就是 R = 1

5. 接著都是同樣動作，把表格給填完，即可得出答案。