今天會著重介紹密碼系統本身,並搭配 SageMath 實作。
NTRU 密碼系統,翻譯為「吾乃數論學家」密碼系統。其實與我們之前討論過的二維晶格密碼系統非常類似。除了加密過程中會有各種模算數以外,解密的正確性也有類似模式:因為係數的大小可以被控制,所以會得到比模數等號還強的整數等號。
我們也趁這時候先講好一些約定符號:
首先我們要考慮以下三個多項式商環
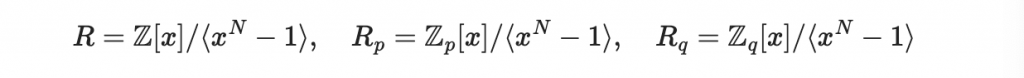
再來,我們要考慮這種集合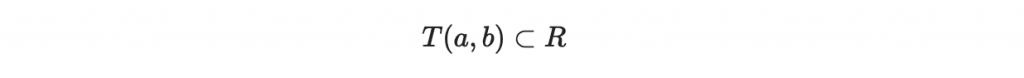
裡面包涵「洽有 a 個係數等於 1、洽有 b 個係數等於 -1、其他係數等於 0 」的所有多項式:例如
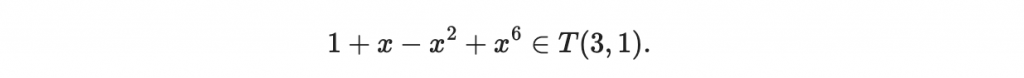
這種集合被稱為「三元多項式」(ternary polynomial)
後續的 SageMath 程式中,我們會使用 ternary_polynomial(a, b, N) 函數來生成這些多項式。
另外我們需要一個重要概念:「有號提升」Center-lift
我們之前講過所謂的「提升」(lift),就是直接把整數商環的整數當作平常的整數來用。如果本來是模除 m 的整數商環,那提升的結果會是落在 0, 1, ..., m-1。
所謂的「有號提升」是指,把每個在模除 m 的整數商環,都提升至以下區間內的整數:
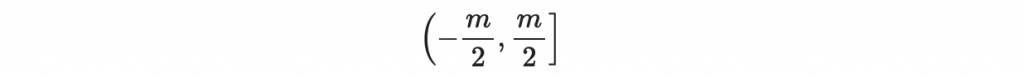
如果你對一個在
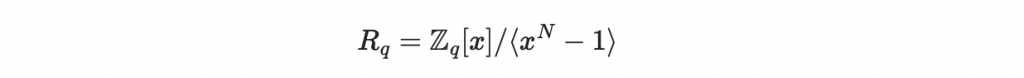
裡面的多項式進行有號提升,其結果就是把每個係數都提升到 (-m/2, m/2] 的區間。
數組 (N, p, q, d)
以上這些可稱為,全域參數(global parameters),是公開資訊的一部分。
# NTRU parameters
N = 11 # degree of the polynomial, should be prime
p = 3 # small modulus
q = 73 # large modulus
d = 2
print(q > (6*d+1)*p)
# Polynomial ring
R_poly = quotient(PolynomialRing(ZZ,x),x^N-1)
R_q = quotient(ZZ,q*ZZ)
R_q_poly = quotient(PolynomialRing(R_q,x),x^N-1)
R_p = quotient(ZZ,p*ZZ)
R_p_poly = quotient(PolynomialRing(R_p,x),x^N-1)
# Outputs:
# True
Alice 隨機生成以下兩個多項式:
並計算
如果上面這兩個皆不存在,重新生成 f
# Ternary polynomial generation
def ternary_polynomial(d1, d2, N):
poly_coeffs = [1]*d1 + [-1]*d2 + [0]*(N-d1-d2)
shuffle(poly_coeffs)
return R_poly(poly_coeffs)
f = ternary_polynomial(d+1,d,N)
g = ternary_polynomial(d,d,N)
F_q = R_q_poly(f)^(-1)
F_p = R_p_poly(f)^(-1)
接著在 R_q 中計算
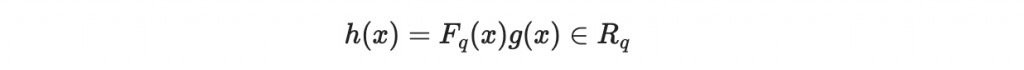
另外 F_p 留作解密使用。(可以要用的時候再計算)
h = F_q*R_q_poly(g)
print(h)
# Outputs:
# 67*xbar^10 + 44*xbar^9 + 55*xbar^8 + 59*xbar^7 + 16*xbar^6 + 36*xbar^5 + 47*xbar^4 + 31*xbar^3 + 71*xbar^2 + 22*xbar + 63
公鑰為:h(x)、以及 (N, p, q, d)
私鑰為:f(x), g(x)
Bob 欲傳加密訊息給 Alice
首先,Bob 將要傳的訊息表示為一個多項式:
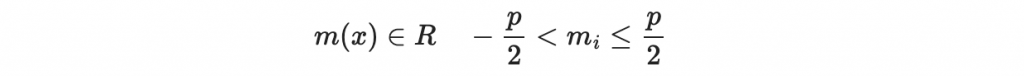
其次,Bob 選擇一個隨機的多項式
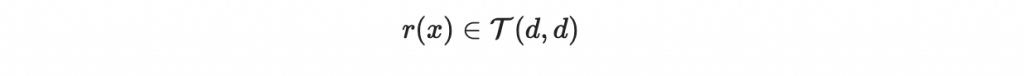
m = R_poly([0,1,0,0,0,1,1])
r = ternary_polynomial(d,d,N)
計算密文:
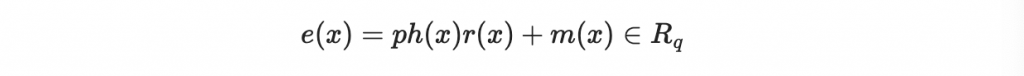
e = p*R_q_poly(h)*R_q_poly(r) + R_q_poly(m)
print(e)
# Outputs:
# 3*xbar^10 + 13*xbar^9 + 27*xbar^8 + 21*xbar^7 + 9*xbar^6 + 58*xbar^5 + 48*xbar^4 + 16*xbar^3 + 38*xbar^2 + 15*xbar + 47
解密:Alice 收到 Bob 傳送過來的 e(x)
在 R_q 中計算
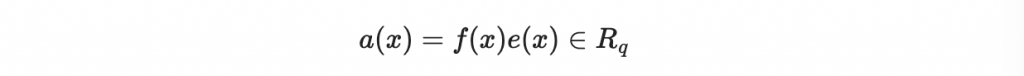
a = R_q_poly(f) * e
print(a)
# Outputs:
# xbar^10 + 72*xbar^9 + 2*xbar^8 + 67*xbar^7 + xbar^6 + 9*xbar^5 + 63*xbar^4 + 72*xbar^3 + 7*xbar^2 + 72*xbar + 2
將 $a(x)$ 做有號提升到 $R$
# Center-lift function
def center_lift(poly, q):
# 先把係數列出來
original_coeff = poly.list()
# 把比 q/2 還大的數字減去 q
center_lifted_coeffs = []
for coeff in original_coeff:
if coeff > (q // 2):
coeff -= q
center_lifted_coeffs.append(coeff)
return R_poly(center_lifted_coeffs)
a = center_lift(a,q)
print(a)
# Outputs:
# xbar^10 + 72*xbar^9 + 2*xbar^8 + 67*xbar^7 + xbar^6 + 9*xbar^5 + 63*xbar^4 + 72*xbar^3 + 7*xbar^2 + 72*xbar + 2
最後在 R_p 中計算
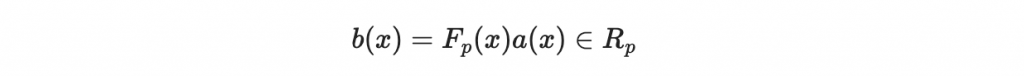
此 b(x) 即等於 m(x)。
a = center_lift(a,q)
print(a)
print(type(a))
# Outputs:
# xbar^10 - xbar^9 + 2*xbar^8 - 6*xbar^7 + xbar^6 + 9*xbar^5 - 10*xbar^4 - xbar^3 + 7*xbar^2 - xbar + 2
# <class 'sage.rings.polynomial.polynomial_quotient_ring.PolynomialQuotientRing_generic_with_category.element_class'>
好!看到這裡,你大概很好奇:「為什麼這樣胡搞瞎搞最後解密會成功?」我們以下開始詳細的數學證明。
首先我們展開多項式 a(x)
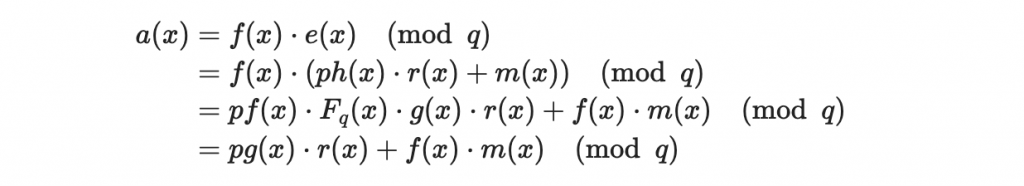
好的,我們來對
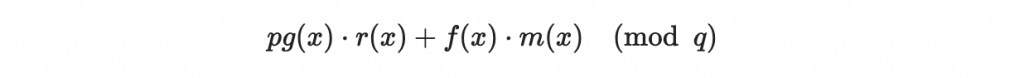
做分析:
首先注意到根據我們的構造, g(x),r(x) 皆屬於 T(d,d),所以乘積 g(x) r(x) 可能的最大係數為 2d 。(這種情況是兩個多項式的 1 與 -1 都互相有配對到的時候)
又注意到 f(x) 屬於 T(d+1,d),而 m(x) 的係數落於
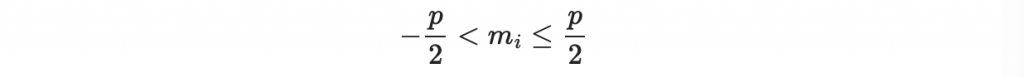
所以乘積 f(x)m(x) 可能的最大係數為 (2d+1)p/2。
因此,
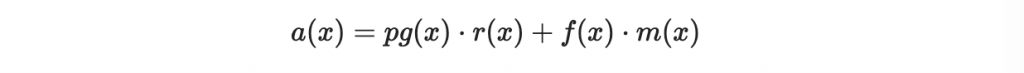
的可能最大係數為
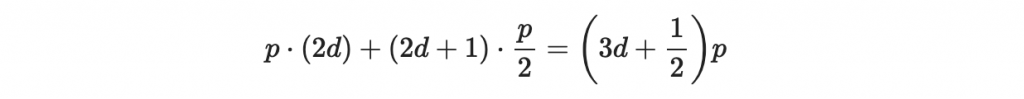
根據我們選擇全域參數設定: (6d+1)p < q ,我們知道
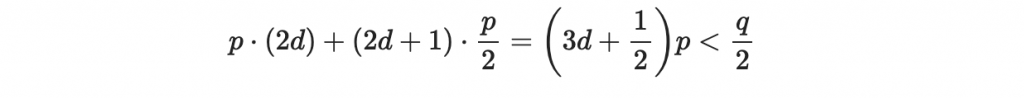
所以當 Alice 計算完 a(x) 並有號提升到 R 時,以下的等式
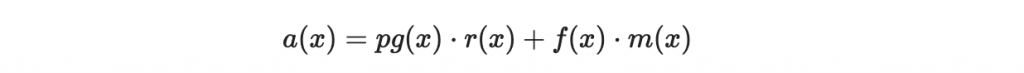
仍然在 R 成立。(注意:根據解密的過程,我們原先只知道在模除 q 之下有以上等式,現在是不需模除 q 而等式仍然成立)
e
接著我們可以繼續做模 p 的運算(在 R_{p} 裡的運算):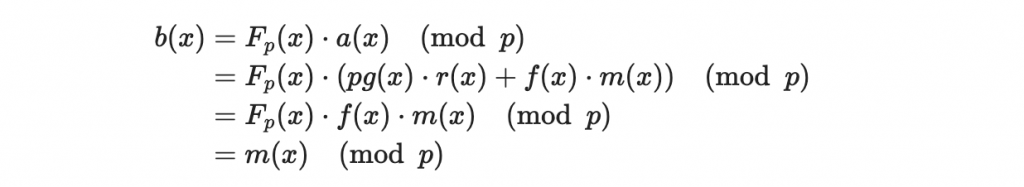
於是,我們可以正確的解碼。
跟當時講二維晶格時類似的事情又發生了,通篇文章沒看到什麼向量之類的符號,這與晶格密碼學有什麼關係?明天我們就來看這個密碼系統的攻擊方法,在這當中就會有晶格問題!
