昨天我們討論了 Hamming Code ，是一個可以非常快速糾正錯誤的編碼系統。今天我們來看一個特別的「多項式編碼」：Reed-Solomon Code

RS 編碼的核心思想是將訊息視為一個多項式，然後在有限域（你可先想成我們之前做的整數商環 Z_q）上對其進行運算。這種方法使得 RS 編碼能夠高效地處理錯誤，並具有靈活的錯誤更正能力。今天我們先討論編碼的部分，明天再來看糾錯機制

RS 編碼系統

首先要選擇參數
k : 訊息的位元數
n : 編碼的位元數
q : 整數商環 Z_q 的模數
其中需滿足

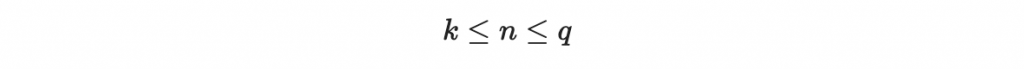
除此之外還需在 Z_q 中選擇 n 個相異的點

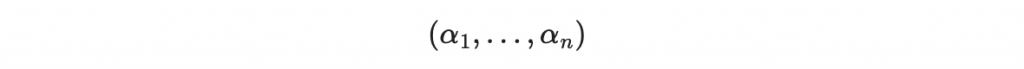
你可以把這些點叫做「插值點」（或者「評估點」）

選擇要傳送的訊息

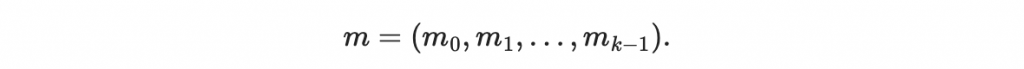
其中 m_i 都是 Z_q 中的點（可以相同）。

編碼方式如下：
生成多項式

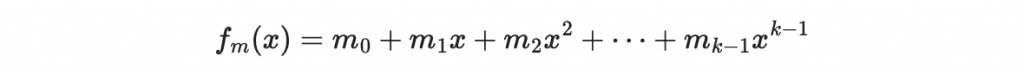
你可以把它叫做「訊息多項式」

然後計算所有 alpha_i 代進去的值

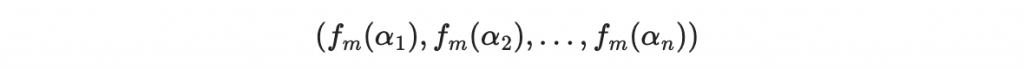
這就完成了 RS 編碼！

生成矩陣

好的，我們進行以下計算

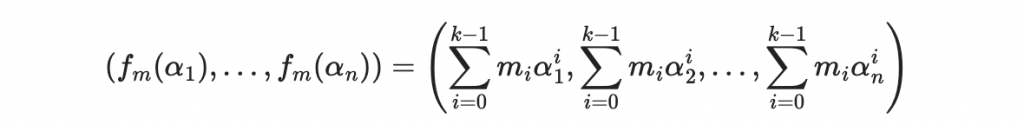
於是可以把碼字寫成 mG ，其中

關於解碼

假設傳遞過程沒有錯誤，從碼字

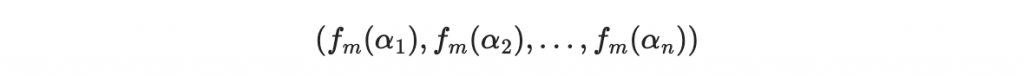
解回 m 就是標準的多項式插值法，最常見的方法莫屬拉格朗日插值法，若你不怕計算麻煩，使用牛頓插值法或任何其他插值法也都可以。

但是當傳遞過程中出現錯誤時，假設最多有 t 個錯誤且收到的字為

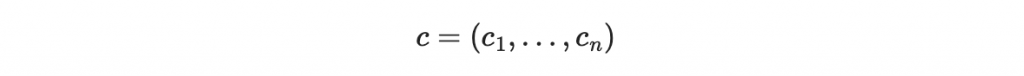
那我們就面臨「在 c 中有最多其中 t 個是錯誤資料其他都是正常的函數值，要找到本來的 k-1 次多項式 f_m 的問題」。乍看之下非常複雜，實際處理起來也是有點麻煩，我們明天再來研究這個糾錯機制。

SageMath 實作

# Parameters:

q = 17
n = 7
k = 3

R = quotient(ZZ, q*ZZ)

alphas = []
while len(alphas) < n:
    elem = R.random_element()
    if elem not in alphas:
        alphas.append(elem)

print(f"插值點: {alphas}")

# Outputs:
# 插值點: [13, 16, 7, 14, 2, 9, 1]

# Generator matrix

G = Matrix(
    R,
    [
        [alphas[i]^j for i in range(n)]
        for j in range(k)
    ]
)
print("生成矩陣 G:")
print(G)

# Ouptuts:
# 生成矩陣 G:
# [ 1  1  1  1  1  1  1]
# [13 16  7 14  2  9  1]
# [16  1 15  9  4 13  1]

message = [R.random_element() for _ in range(k)]

print(f"訊息: {message}")

# Outputs:
# 訊息: [6, 3, 1]

def encode(message):
    return (Matrix(message) * G).list()

encoded = encode(message)

print(f"編碼: {encoded}")

# Outputs:
# 編碼: [10, 4, 8, 6, 16, 12, 10]

Takeaway

• 多項式編碼很籠統地來說就是使用多項式這個數學物件所做的編碼，一個重要的例子就是 Reed-Solomon Code
• Reed-Solomon 的編碼方式是將訊息作為係數來產生一個多項式，然後把插值點帶進去。

ref:
GURUSWAMI, Venkatesan; RUDRA, Atri; SUDAN, Madhu. Essential coding theory.