堆積（Heap） 是一種特殊且完整的二元樹，可分為最大／小堆積樹兩種。最大堆積樹中所有節點的值都大或等於它左右子節點的值，這兩種樹的樹根（root）是其堆積樹中最大的；而最小堆積樹亦同理。而堆積排序法就需要建立或將二元樹換成堆積樹來做堆積排序演算法。而當需要取得升序（由小排到大）的節點排序，就需要建立最小堆積樹；反之，若需要取得降序（由大排到小）的節點排序，就需要建立最大堆積樹。以下範例將介紹如何將二元樹轉換成堆積樹、並且建立堆積樹後如何做堆積排序：

堆積排序法小Tips:

• 在所有情況下，時間複雜度均為O(nlogn)
• 堆積排序法不是穩定排序法（只要兩相鄰值大小相等，兩者的相對位置就不會改變。）

範例說明一：如何將一般二元樹轉換為堆積樹？（此題以最大堆積樹為例）

問題說明：假設有8筆資料34、19、40、14、57、17、4、43，我們以二元樹表示如下：
現在要將此二元樹轉換為最大堆積樹，我們可以用陣列來儲存二元樹所有節點A[0]=34、A[1]=19、A[2]=40、A[3]=14、A[4]=57、A[5]=17、A[6]=4、A[7]=43。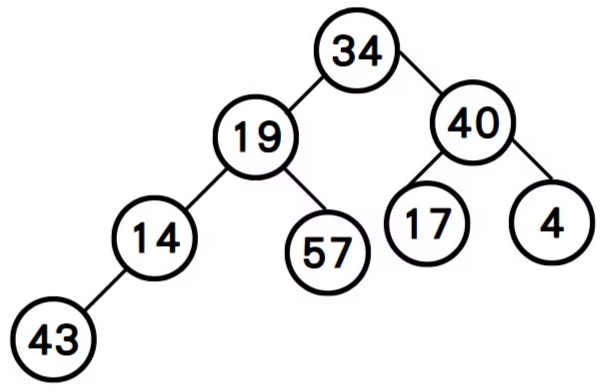

step1: 二元樹中最大的元素為A[4]=57，需要將其依序換至樹根的位置。先與A[1]=19交換，再與A[0]=34交換。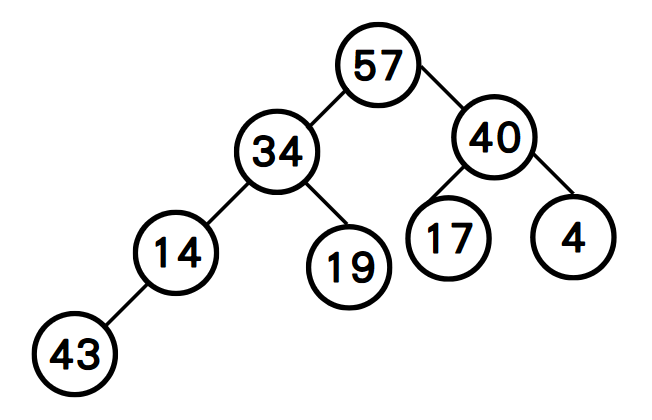

step2: 找到第二大的元素A[7]=43，先與A[3]=14交換，再與A[1]=34交換。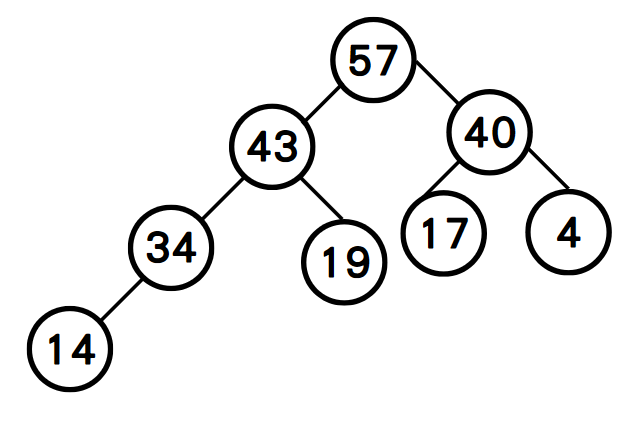

step3: 接下依序檢查第三大、第四大…等元素，發現皆小於其父節點，故無需更換。堆積樹完成！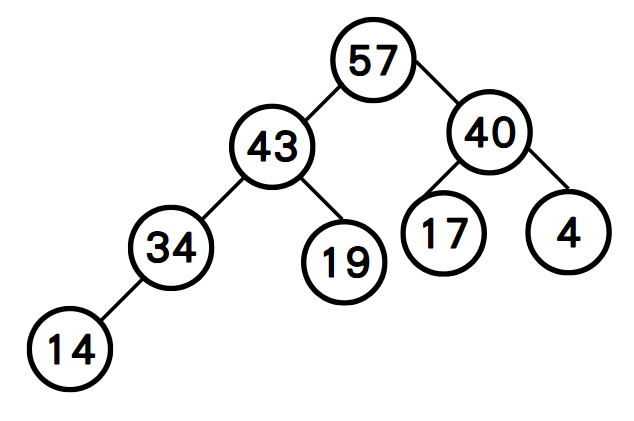

範例說明二：（續範例一）如何將轉換好的堆積樹作堆積排序？

step1: 將57自樹根移除，重新建立堆積樹。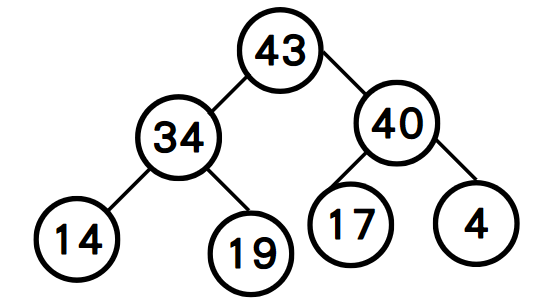

step2: 將43自樹根移除，重新建立堆積樹。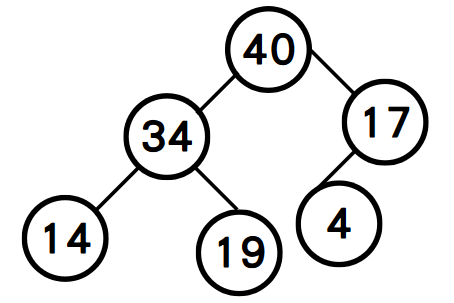

step3: 將40自樹根移除，重新建立堆積樹。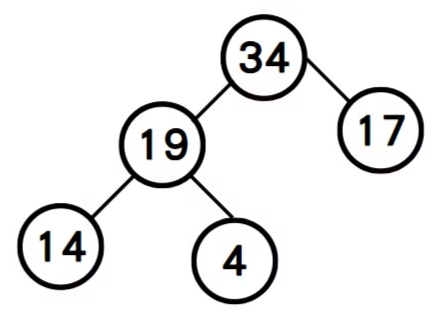

step4: 將34自樹根移除，重新建立堆積樹。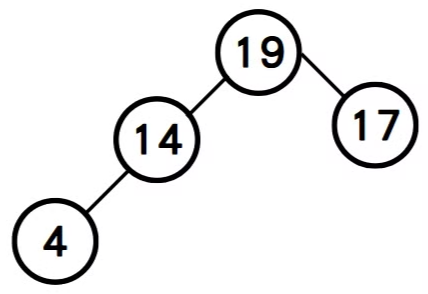

step5: 將19自樹根移除，重新建立堆積樹。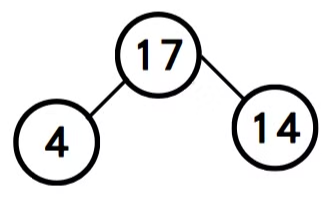

step6: 將17自樹根移除，重新建立堆積樹。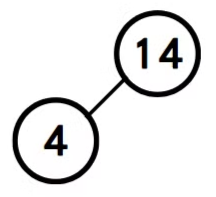

step7: 將14自樹根移除，重新建立堆積樹。

最後將4自樹根移除，得到排序為57、43、40、34、19、17、14、4。

優點：

• 高效處理最大值或最小值：Heap 是一個完全二元樹，能在 O(nlogn) 的時間內插入新元素或取出最大（或最小）元素。因此，在需要頻繁取得最大值或最小值的情況下（如優先隊列），Heap 表現非常出色。
• 穩定的時間複雜度：不論資料是否已排序，Heap 的插入和刪除操作時間複雜度始終為 O(nlogn)，相對穩定。
• 應用廣泛：Heap 被廣泛應用於許多演算法中，如 Dijkstra 最短路徑、Kruskal 最小生成樹、Huffman 編碼等。

缺點：

• 排序效率不如快速排序：Heap 排序的時間複雜度是 O(nlogn)，而快速排序在大多數情況下的時間複雜度為 O(nlogn)，但具有較小的常數因子，通常比 Heap 排序更快。
• 需要額外的空間：Heap 通常需要用到額外的資料結構來維護優先順序，特別是在實作二元堆時，會使用陣列或鏈結結構來儲存節點。
• 隨機存取不方便：Heap 不適合隨機存取元素，因為其結構是基於父子關係進行組織的，無法像陣列一樣直接透過索引存取指定位置的元素。

參考資料：

1. 李春雄(2021)。《動畫圖解APP資料結構─使用Java》。台中：滄海出版。
2. 吳燦銘、胡昭民(2018)。《圖解資料結構-使用Java(第三版)》。新北：博碩文化。
3. 吳燦銘、胡昭民(2020)。《圖說演算法：使用Java》。新北：博碩文化。
4. 演算法學習筆記：氣泡排序（Bubble Sort）、插入排序（Insertion Sort）、選擇排序（Selection Sort） - Medium by 拉爾夫的技術隨筆
5. [資料結構] 堆積 (Heap) - iT邦幫忙 by ramonliao