堆積 (Heap),是一種特殊的完全二元樹,而堆疊不一樣,是完全不同的概念。
有分兩種,一種是最小堆積,另一種是最大堆積。
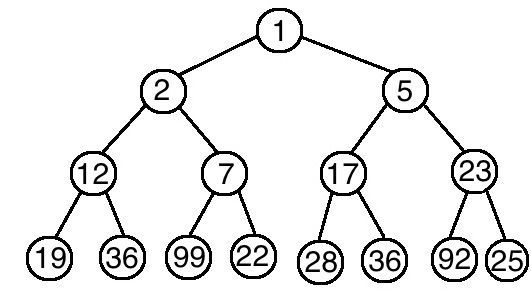
如下圖,完全二元樹所有的父節點都比子節點要小,就屬於最小堆積。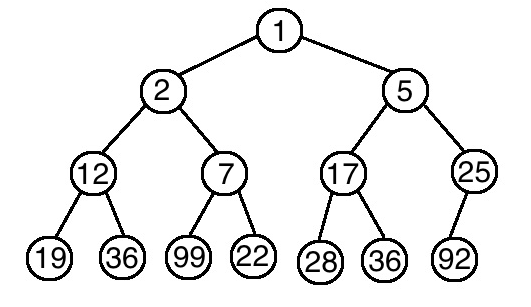
若完全二元樹所有的父節點都比子節點要大,則為最大堆積。
(以下用最小堆積來討論。)
怎麼建立呢?首先將資料存入到完全二元樹當中,再來一一調整以符合堆積的特性。從最後一個節點開始,依次判斷以這個節點為根的子數是否符合最小堆積的特性。一層一層往上判斷調整,直到整棵樹都符合為止。
1 2
2
3 4
4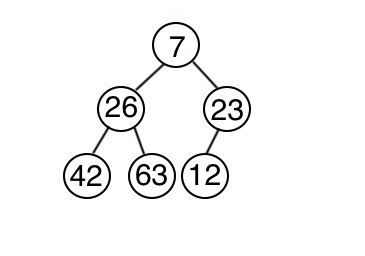
5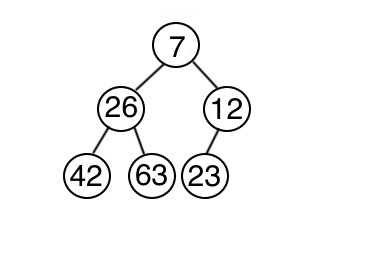
如果要搜尋指定節點,只要用迴圈從頭掃一次就可以解決,時間複雜度是 O(N)。刪除也是一樣的概念,但執行上就不太一樣了。
在最小堆積中,如果刪除的是最小的數,理論上來說就會是在樹的頂端,若堆積的陣列叫做 h 的話,最小樹就是 h[1] 了。然後從右子樹網上遞補。但若父節點大於子節點的話,則要往下持續調整,直到樹符合最小堆積。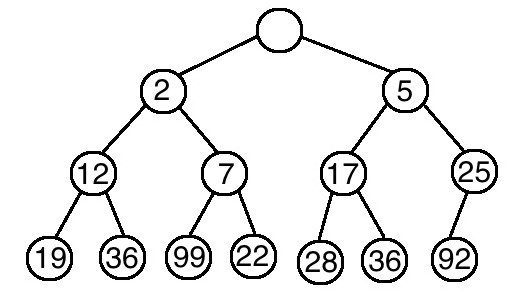
若刪除了最小數,接著要插入一個數,我們可以從頂端開始,向下比較,取左右子樹較小的值與之交換,再一一往下重複施作,直到符合最小堆積為止。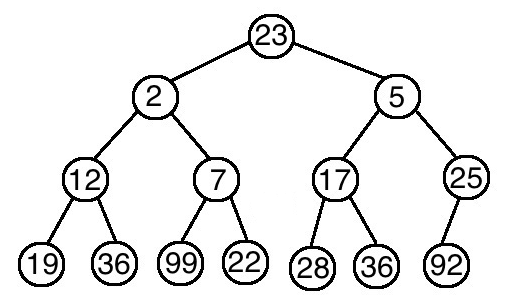
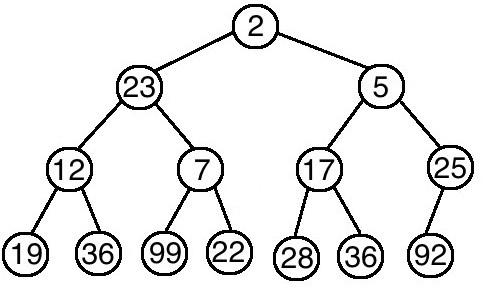
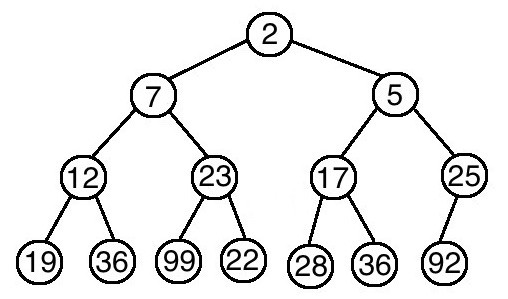
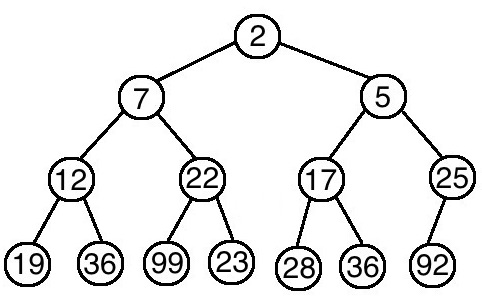
那又如果沒有刪除,直接插入新元素呢?我們可以將它插在樹的末尾,再根據情況判斷新元素是否需要上移,直到滿足堆的特性為止。如果堆的大小為N,那插入一個新元素所需的時間為 O(logN)。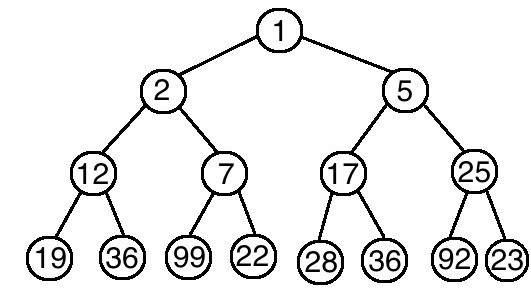
堆積也可以用來排序。假設一個陣列 h,有 n 個元素,我們要由小排到大,可以先建好最小堆,然後每次刪除頂端元素並放到一個新的陣列,直到整棵樹圍空,最終輸出新的陣列就是排序好的陣列。data = []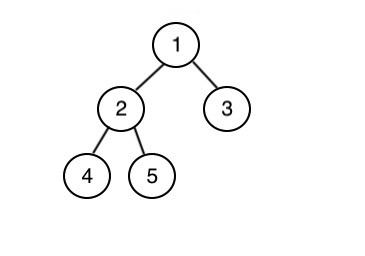
data = [1]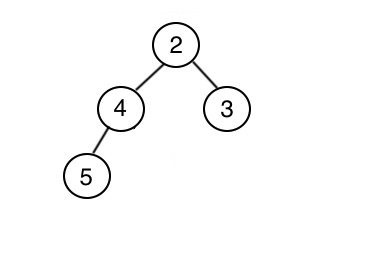
data = [1, 2]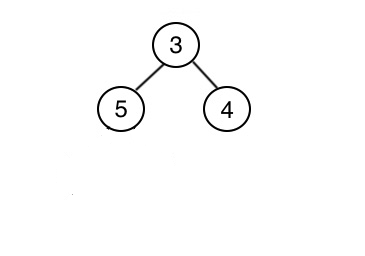
data = [1, 2, 3]
data = [1, 2, 3, 4]
data = [1, 2, 3, 4, 5]
另一個方法,我們要從小到大排序,但建立的是最大堆積而不是最小堆積。此時最大堆積的頂端 h[0] 是最大元素,則將 h[0] 與 h[n] 互換,最大的就在陣列的尾端了。這時候新換好的 h[0] 再向下調整,直到 h[n-1] ,以保持最大堆積的特性,調整完再將 h[0] 與 h[n-1] 互換。這時候重複以上動作直到 n-1 = 0 的時候,就代表陣列排序了。
有興趣的可以自己拿筆畫畫看,或寫成程式運行看看喔!
