前幾天介紹許多數據匿名方法，許多其實都可以依靠「外部訊息」破解，但是！這篇特別提出的手段，是比其他技術有更全面且強大的保護能力。
可以在收集群體資料的同時，保護個體數據，核心思想是：無論某人的數據是否存在於數據集中，當你對這個數據集進行查詢時，查詢結果的差異應該微乎其微。(這個「基本一致」的結果保證了攻擊者無法從查詢結果中推斷出某個特定個體是否參與了數據集)，簡單來說，若無法分辨一個演算法的輸出是否使用了某一特定個體的資訊，這樣的演算法就是差分隱私的。

ε值的設計:

使用參數 ε(epsilon) 來度量隱私的“泄漏”程度 ;ε越小，保護越強，但這也可能減少數據的精確度，因此，差分隱私提供了一個隱私與數據效用之間的平衡點，根據應用情況選擇適合的ε值來決定保護力。

[wikipedia定義]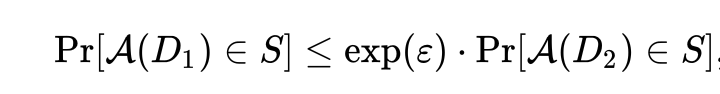

其中 \exp(\epsilon) 表示機制在兩個鄰近數據集上的結果可能出現的最大差異，當 \epsilon 越小，這個放大係數越接近1，即兩個數據集上的結果幾乎一致，隱私保護越強。

噪聲機制(Noise Mechanism)😮:

差分隱私依賴於向數據中添加隨機噪音，通常使用拉普拉斯噪聲(Laplace Noise)、高斯噪聲機制。

[wikipedia 機率密度函數]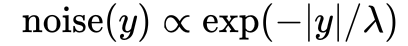

其中的\lambda 是一個尺度參數，控制噪音大小。
拉普拉斯機制在查詢結果上添加的噪音量是基於敏感度（Sensitivity）來決定的。
(＊靈敏度(Sensitivity)：操作結果對數據集中個體的變化有多敏感)

組合性(Composability)🧦：

差分隱私具有可組合性，當多次對同數據集進行查詢時，隱私的「耗損」是累積的。
(耗損(privacy loss)：是指在進行多次查詢或數據分析時，對個體隱私的保護程度隨著查詢次數的增加而減少的現象)
組合性使得整體隱私損失是可以預測，可以根據每次查詢的ε值來計算總損失，從而確保在可接受範圍內。

我們熟知的一些科技公司(如Apple、Google)在其產品中也有實施差分隱私，明天可能針對apple的運用方面進行舉例，讓我們更了解這些概念到底怎麼運作，光看公式也有點難懂，但也可能直接進入下個概念🥸。