DAY 12 試題

問題描述

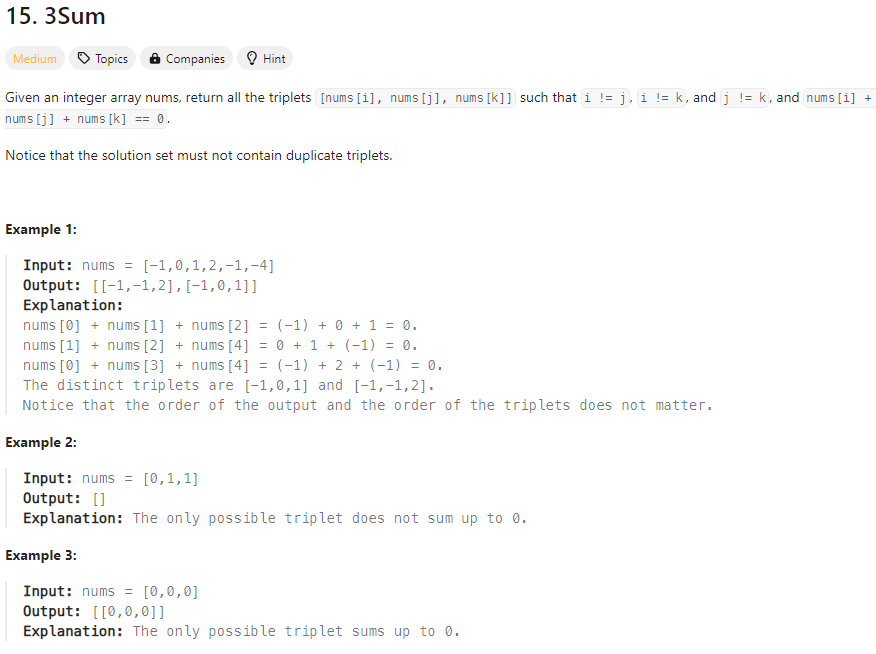
給定一個整數陣列 nums，要求找出所有三元組 [nums[i], nums[j], nums[k]]，使得：

1. i != j、i != k 且 j != k。
2. 三個數字之和為 0，即 nums[i] + nums[j] + nums[k] == 0。
   需要注意的是，解答集合中的三元組必須是唯一的，不得包含重複的三元組。

範例 1：

• 輸入: nums = [-1,0,1,2,-1,-4]
• 輸出: [[-1,-1,2],[-1,0,1]]
• 解釋：在這個陣列中，兩組符合條件的三元組為 [-1, 0, 1] 和 [-1, -1, 2]。

範例 2：

• 輸入: nums = [0,1,1]
• 輸出: []
• 解釋：無法找到任何三個數字加總為 0。

範例 3：

• 輸入: nums = [0,0,0]
• 輸出: [[0,0,0]]
• 解釋：只有一組符合條件的三元組 [0, 0, 0]。

限制條件：

• 3 <= nums.length <= 3000
• -10^5 <= nums[i] <= 10^5

解題思路

這是一道經典的「三數之和為 0」問題，核心是如何有效地避免重複計算並保持結果的唯一性。最直觀的暴力解法是三層迴圈遍歷所有三元組，時間複雜度為 O(n^3)，但對於最大 3000 長度的陣列來說，這個解法會太慢。因此，我們可以優化這個解法，降低時間複雜度至 O(n^2)。

解題的具體步驟如下：

1. 排序：首先將陣列 nums 進行排序。這可以幫助我們在處理重複元素時更有效。

2. 雙指針法：利用一個變數 i 固定一個數字，然後使用雙指針來找出另外兩個數字。具體做法是從 i+1 到結尾設置兩個指針，一個指向頭部 (left)，一個指向尾部 (right)，這樣可以通過計算三者的和來判斷是否需要移動指針。

3. 處理重複數字：為了保證結果唯一，我們在移動指針和固定變數 i 時，都需要跳過重複的數字。

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> result;
        sort(nums.begin(), nums.end()); // 先排序
        int n = nums.size();
        
        // 固定第一個數字 i
        for (int i = 0; i < n - 2; ++i) {
            // 跳過重複的數字
            if (i > 0 && nums[i] == nums[i - 1]) continue;
            
            int left = i + 1;
            int right = n - 1;
            
            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right];
                
                if (sum == 0) {
                    result.push_back({nums[i], nums[left], nums[right]});
                    
                    // 跳過重複的數字
                    while (left < right && nums[left] == nums[left + 1]) left++;
                    while (left < right && nums[right] == nums[right - 1]) right--;
                    
                    // 移動指針
                    left++;
                    right--;
                } else if (sum < 0) {
                    left++; // 如果和太小，移動左指針
                } else {
                    right--; // 如果和太大，移動右指針
                }
            }
        }
        
        return result;
    }
};

解法重點與分析

1. 排序與雙指針技術的結合：這道題的關鍵在於將原始數組進行排序後，使用雙指針來找到和為 0 的三元組。排序的時間複雜度是 O(n log n)，而每次固定一個數字後，用雙指針在剩下的數字中尋找符合條件的另外兩個數字，這部分的時間複雜度是 O(n)。總體來看，解法的時間複雜度是 O(n^2)，這比起暴力解法的 O(n^3) 有顯著的提升。
2. 避免重複三元組的處理：為了避免結果中出現重複的三元組，我們在固定一個數字 nums[i] 時，當前後數字相同時跳過這個數字。同樣地，雙指針在進行左右移動時也要跳過重複的數字，這樣保證了每個三元組的唯一性。
3. 時間複雜度：排序的時間複雜度為 O(n log n)，雙指針的搜尋是 O(n)，總體上來說，整個算法的時間複雜度為 O(n^2)。
4. 空間複雜度：由於我們僅僅使用了少量額外的變量來進行指針操作，因此空間複雜度為 O(1)（不考慮輸出結果所佔的空間）。
5. 處理極端情況：針對 nums 長度小於 3 的情況，直接返回空結果；而對於含有多個相同數字的情況（例如 [0, 0, 0]），我們也通過跳過重複數字來確保結果的正確性。

總結

這道題通過排序和雙指針技術，有效降低了時間複雜度至 O(n^2)，同時通過跳過重複數字來保證結果的唯一性。這樣的解法不僅適用於三數之和的問題，也可以推廣至其他類似的數組問題，是一種高效且常用的技巧。

以上是第十二天的自學內容分享，謝謝大家。