離散型分配 PMF

若有一隨機變數 X 的樣本空間為可數，則稱隨機變數 X 為離散型分配（Discrete Probability Distribution）。-- Statistical Inference，George Casella and Roger L. Berger，85頁。

嚴格來說，連續型隨機變數的分配函數稱作機率密度函數 PDF；而離散型隨機變數的分配函數稱作機率質量函數 PMF。但有些地方會以 PDF 來概稱兩者。本文採取嚴格的定義，分開稱呼 PDF 與 PMF。

連續型隨機變數與離散型隨機變數的最大不同之處在於：前者的單點機率，例如：$x = 0$ 的機率，為零，需在一段樣本區間內透過積分計算才有大於零之機率值；而後者在樣本點上的單點機率大於零，本身代表該樣本點時的機率。以下介紹離散型分配，及其對應之機率質量函數 PMF。

Negative Binomial 負二項分配

Negative Binomial Distribution 的中文稱作負二項分配，係「持續進行伯努力試驗，其成功機率 p，直至得到第 n 次成功才停止，總共的失敗次數 X」（有另一定義為「... ，總共的試驗的次數」，本文使用前者：失敗次數），記作 X ~ NB(n, p)。

失敗次數 X，其 PMF 可以表示為

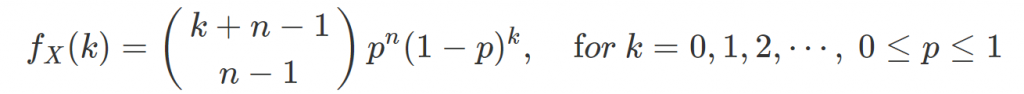
相關的 PMF 由來的推導可見：負二項分布、負二項式分布，文中還有說明負二項名稱的由來。

Negative Binomial 分配在 Python 的 PMF 程式碼為 binorm.pdf，其數式如上式。設定 n=30 與 p=[0.45, 0.5, 0.55] 畫該分配的 PMF 與 CDF，如下圖，觀察此圖， p 為影響偏度的重要因子，隨 p 越大，則右側的尾部更長，使平均數在眾數的更右側。即 Negative Binomial 分配隨 p 越大，分配越右偏。

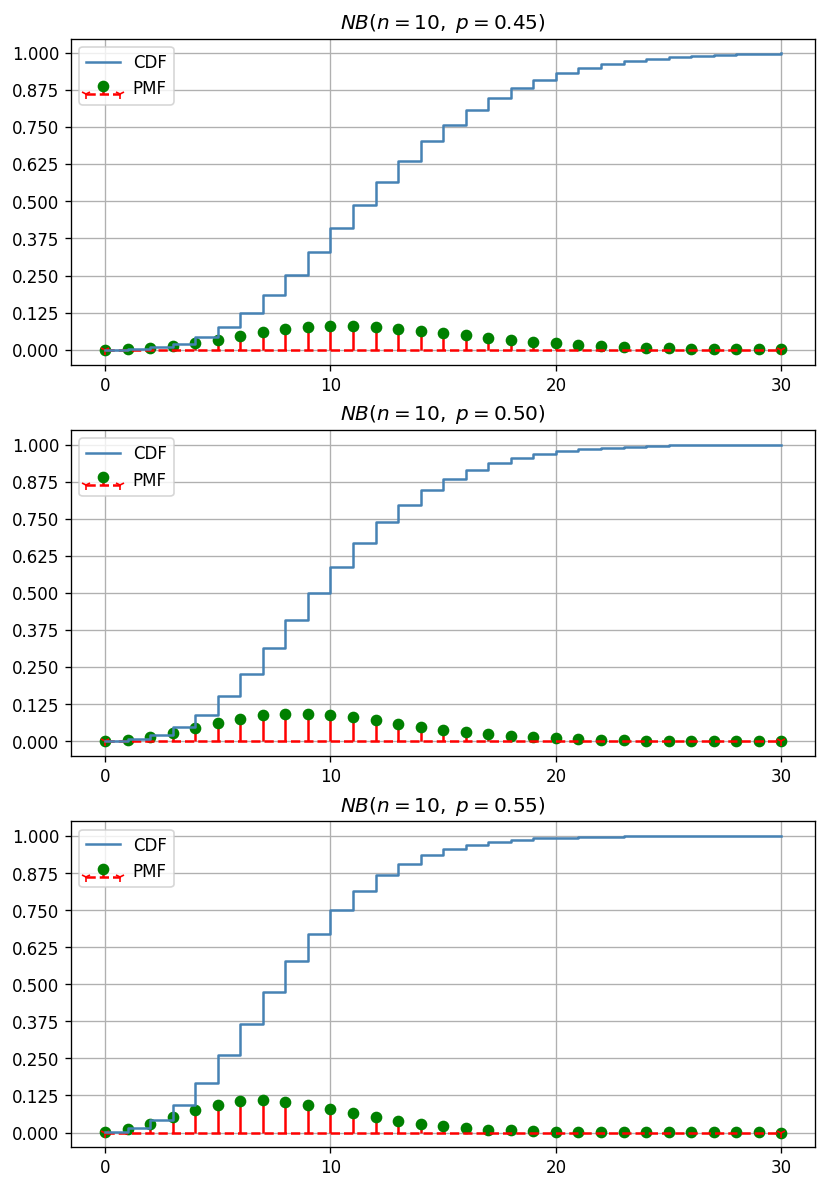
Python 程式碼如下，畫 Negative Binomial 的 PMF 與 CDF 圖時，需要傭有一些選擇參數的小技巧，才可以較好表現 Negative Binomial 的特性。此處設定 n, p 的相對大小要剛剛好，才可以讓 PMF 與 CDF 在 k 的數值仍不大時就呈現大部分的函數特徵。另外，圖片中樣本點的最大範圍不是只到 30，而是因圖片版面限制而選擇畫到 30。實際上，如 PMF 的 k 之上界 ，樣本點的最大範圍為無限大的正整數。同理，其 CDF 也到無限大的正整數時才會真正為 1。

# Negative Binomial

from scipy.stats import nbinom

fig, ax = plt.subplots(3, 1, figsize=[8, 12], dpi=120)

n = 10 # 試驗停止前，成功的次數
x = np.arange(3 * n + 1) 

prab = 0.45 # 取接近 0.5 讓圖形可以在較小的 x 範圍內表現
p = [prab, 0.50, 1 - prab] # 單次試驗成功的機率

for i in range(len(p)):
  # PMF
  y = nbinom.pmf(x, n, p[i])
  ax[i].stem(y, linefmt='r-', markerfmt='go', basefmt='r1--', label='PMF')
  # CDF
  Y = nbinom.cdf(x, n, p[i])
  ax[i].plot(Y, drawstyle='steps-post', color='steelblue', label='CDF') # <<< drawstyle='steps-post'

  ax[i].set_xticks(np.arange(0, 3 * n+10, 10)) 
  ax[i].set_title(r'$NB(n={}, \ p={:.2f})$'.format(n, p[i]))
  ax[i].set_yticks(np.arange(0, 1+0.25/2, 0.25/2))
  # ax[i].set_yticks(np.concatenate((np.array([0, 0.125]), np.arange(0.25, 1+0.25, 0.25))))
  ax[i].grid(True)
  ax[i].legend()

plt.show()

Geometric 幾何分配

Geometric Distribution 中文稱作幾何分配，可以視為 Negative Binomial 分配的一種特殊形態。若將 Negative Binomial 分配取 n = 1，則可以得到

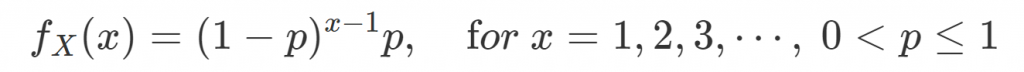
定義 Geometric 隨機變數 X 的 PMF。其中參數 p 為成功的機率。另外，隨機變數 X 可以看作「直到第一次成功事件發生，總共的試驗次數」，或也可以解釋為「直到第一次成功發生所等待的次數」，都是在等待一次的成功發生，記作 X ~ Geo(p)。而其中 p 不可為 0 ，這是因為使此分配的期望值（一階動差）存在，意即使 E|X| < ∞。

此外，Geometric 分配還具有另一個形式，為「第一次成功發生前所經歷的失敗次數」，其可定義為隨機變數 Y = X-1，也就是：把直到第一次成功發生總共的試驗次數減去成功的那一次。本文以 Geometric 分配的第一個形式為主，即隨機變數 X，說明 Geometric 分配的特性。

下圖為設定 p = [0.2, 0.5, 0.8] 下，Geometric 分配的 PMF 與 PDF。可以觀察到 Geometric 分配長的很像 Negative Binomial 分配，這是因為剛提到 Geometric 分配為 Negative Binomial 分配之特例，一樣為右偏分配。

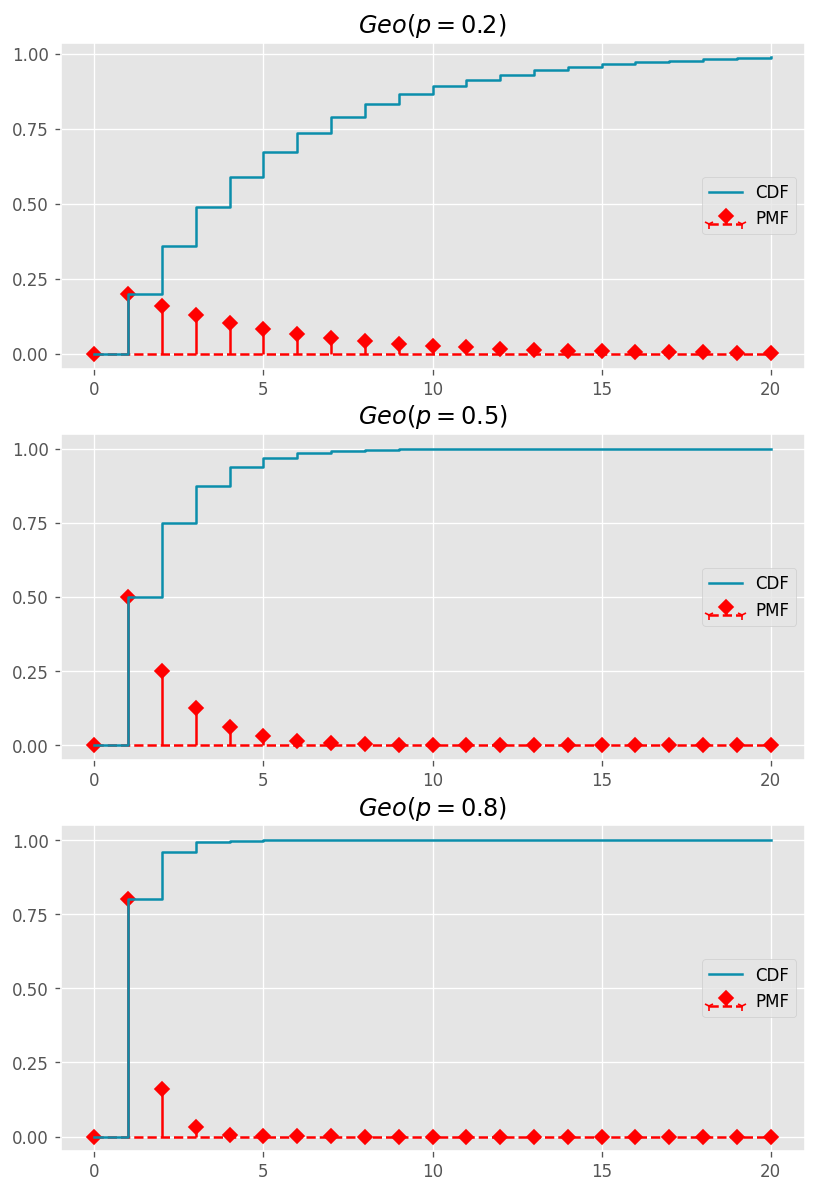
Python 程式碼如下，風格使用 plt.style.use('ggplot') 來套用 R 語言中 ggplot 的繪圖風格，其他可直接套用的繪圖風格可以 plt.style.available 查詢。或是如果畫出如經濟學人雜誌中圖片的風格，雖不能直接使用一行程式碼套用，但可參考下列文章來繪圖：

• Making Economist-Style Plots in Matplotlib
• Narrative Data Visualisation
• The Economist visual styleguide

# Geometric

from scipy.stats import geom

fig, ax = plt.subplots(3, 1, figsize=[8, 12], dpi=120)

n = 20 
x = np.arange(n + 1)

p = np.linspace(0.2, 0.8, 3) # 設定參數 p 

plt.style.use('ggplot') # 套用 R 語言的 ggplot 繪圖風格

for i in range(len(p)):
  # PMF
  y = geom.pmf(x, p[i])
  ax[i].stem(y, linefmt='r-', markerfmt='D', basefmt='r1--', label='PMF')
  Y = geom.cdf(x, p[i])
  ax[i].plot(Y, drawstyle='steps-post', color='#0b8eab', label='CDF')
  ax[i].set_xticks(np.linspace(0, n, 5))
  ax[i].set_title(r'$Geo (p={})$'.format(p[i]))
  ax[i].set_yticks(np.arange(0, 1+0.25, 0.25))
  ax[i].legend(loc='center right')

plt.show()