QDA （Quadratic Discriminant Analysis）

QDA 的概念類似 LDA，但假設各群組的共變異數矩陣不全相同，即各組的共變異數矩陣不可再直接使用 Σ ，而要改以各群組的共變異數矩陣 Σk 分別表示，其中下標代表群組 k。因為最後分析的得到的分界線不是直線，而是變數二次方程式，二次的應為為 Quadratic，故此方法稱作 QDA。

QDA Assumption: multivariate normal with heterogeneous variance-covariance matrices

承續上篇文章對 LDA 的相關介紹，本文從 QDA 的假設開始，推導 QDA 的判定函數，並利用分 2 組群組，呈現 QDA 的決策邊界最高次為二次方。

QDA 之判定函數（Discriminant function）

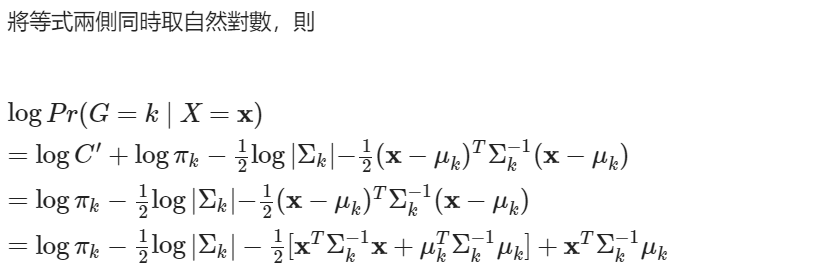
為求所在之群組

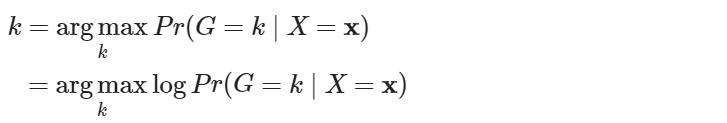
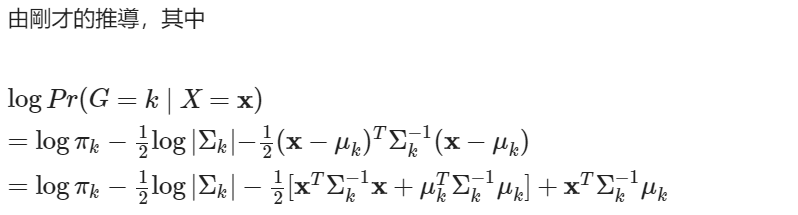
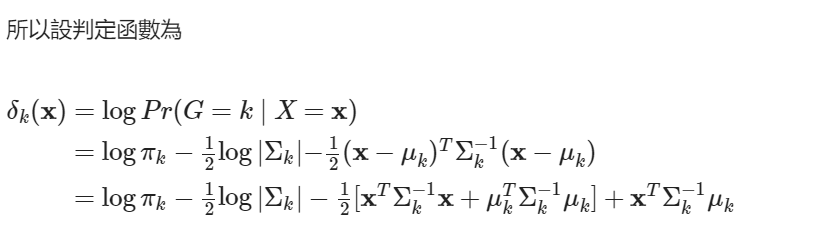
以判斷資料所屬之群組。其中，為後續推算，保留兩種型式的判定函數。第一種型式為具原先多變量常態分配 PDF 的二次式部分結構之型式，而第二種型式為第一種再化簡後的型式。取第一種型式表示決策邊界的樣本集合。

決策邊界（Decision boundary / Decision surface）

QDA 的群組分界線是如何畫出來的呢？跟上篇文章一樣，理論的關鍵在於找出群組間的共同條件，在此為取後驗機率相等的樣本集合為決策邊界。經一些推導，得知多群組下的決策邊界

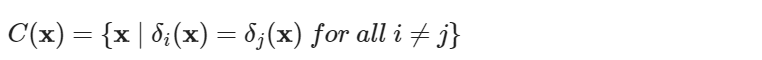
為樣本之子集合。另外，決策邊界在此長得很像數理統計學中假設檢定的 Critical Region 或稱 Reject Region 的樣子，後者為拒絕虛無假設的樣本子集合。儘管兩者長的相像，都是樣本在某些條件下的集合，決策邊界與 Reject Region 的差別在於：後者的補集合稱做 Accept Region，為接受虛無假設的樣本子集合；但前者的補集合可能是任意群組所在地，在分群上沒有什麼涵義。

小結

QDA 的對資料的分群原理跟 LDA 類似，差別在於對後驗機率密度函數的假設不同。前者假設資料的後驗機率密度函數為具不全相同之共變異數矩陣，而後者假設為具相同之共變異數矩陣。儘管兩者在假設上只有些許的不一致，卻使之後的經層層推論出來的的判定函數與決策邊界出現差異。

下一篇文章會承接本文，繼續介紹 QDA ，以兩群組資料分群的例子說明 QDA 名稱中 Quadratic 的由來。另外也向讀者分享一些在跟 QDA 相關的重要數學與統計概念，一切都放在下篇文章的最後。期待讀者可以從所列舉的參考資料中挖掘寶藏，對 LDA 與 QDA 有更深入瞭解，盡情享受數學之美！