先前提到的 Bubble Sort / Insertion Sort / Selection Sort
其 Big O 皆為 O(n^2)，當 dataset 很大的話，效率並不好

那麼，是否所有 sorting algorithm 的 Big O 都是 O(n^2) 呢？
其實並不盡然

今天來介紹 Merge sort

Merge Sort

Merge Sort is a divide and conquer algorithm that recursively splits the dataset into smaller sub-arrays back together while sorting them, continuing this process until the entire dataset is merged and sorted.

Merge Sort 相較於先前介紹的幾種排序演算法步驟上更複雜一些，應用了 分而治之(divide and conquer) 的概念
主要分成三步驟 divide, conquer and combine
先將 dataset 遞迴分割到僅剩1個元素的子集合（僅有1個元素的 sub-set 可視為 sorted）
再將所有子集合排序，最後合併回完整的 dataset

灰色階段為 divide / 綠色為 sorted & merge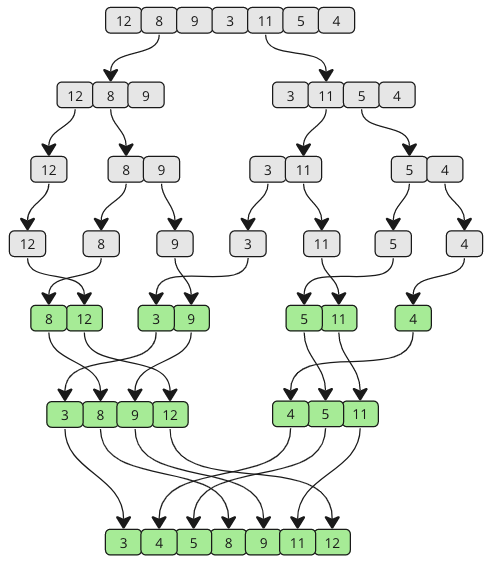

圖片來源

Steps of Merge Sort

1. Pick the middle index
   Divide the dataset into two halves using the middle index.This splits the dataset into a left and right subset.

先取得 dataset 中央的索引值，將 dataset 分為左右個子集合

2. Recursively split the subsets
   Continue spliting each subset in half until each subset has only one element.

持續將子集合分割到直到集合內的元素只剩一個

3. Merge the sorted subsets
   Use two pointers, one for each subset. Compare the elements at these pointers, adding the smaller value to a new result array. Move the pointer of the subset with the small value forward by one.

為每個子集合分別建立一個 pointer，比較兩者 pointer 的值，將較小的值加入到結果的 array 中，並將值較小的子集的 pointer 往前移動ㄧ位

4. Combine the final result
   Once all elements from both subsets are merged, combine them into final sorted array and return the result.

合併兩個子集中的所有元素，將它們組合成最終的 sorted array 並回傳

Complexity of Merge Sort

Best case:O(n * log n)
Worst case:O(n * log n)

Implementation of Merge Sort

Merge sort need two function to complete the work.
The merge function working for merge two subsets; while the mergeSort function works for divide the dataset recursively.

• note: array.slice returns the shallow copy of a portion of the original array into new array select from start to end (end is not included).

let unsortedArr = [4, 8, 3, 6, 10, 5, 7, 1, 18, 12, 13, 9, 2, 11];

function mergeSort(arr){
    if(arr.length <= 1){
        return arr;
    }
    const middleIndex = Math.floor(arr.length/2);
    const leftPart = arr.slice(0 ,middleIndex);
    const rightPart = arr.slice(middleIndex);
    
    return merge( mergeSort(leftPart), mergeSort(rightPart));
}

function merge(leftPart,rightPart){
    let leftStart =0,rightStart =0;
    const result=[];
    
    while(leftStart< leftPart.length && rightStart < rightPart.length){
        if(leftPart[leftStart] < rightPart[rightStart] ){
            result.push(leftPart[leftStart]);
            leftStart++;
        }else{
            result.push(rightPart[rightStart] );
            rightStart++;
        }
    }
    
    return result.concat(leftPart.slice(leftStart)).concat(rightPart.slice(rightStart));
}


console.log(mergeSort(unsortedArr)); // ) [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 18]

Advantage & disadvantage of Merge sort

Advantage:

• Efficiently sort a list in O(n*log(n)) time, no matter worse case or best case

• 最好情況跟最壞情況，其Big O皆為 O(n*log(n))

Disadvantage:

• For small datasets, merge sort is slower than other sorting algorithms

• For the temporary array, merge sort requires additional space of O(n)

• Even if the array is sorted, the merge sort still goes through the entire process.

• 對於處理小的 dataset ， Merge sort 所需的時間比其他排序演算法來的久

• Merge sort 需要額外 O(n) 的空間來存取

• 即使 dataset 已被排序好，Merge sort 仍會執行整個分割與合併的過程

相關資源

Merge Sort Explained
https://developer.nvidia.com/blog/merge-sort-explained-a-data-scientists-algorithm-guide/
merge sort
https://www.w3schools.com/dsa/dsa_algo_mergesort.php