昨天介紹了寐偲,阿天卷Math.atan()給大家使用,知道一個斜率,我們就能透過他來得到相對應的角度;今天要練習的是阿天卷二世Math.atan2()!
寐偲,阿天卷,吐!!!
我們來看看他跟Math.atan()究竟有什麼不同吧!
如果今天我們只有本來的atan函數,那丟給他一個斜率y / x然後回傳一個角度,好像沒有什麼需要特別注意?
錯誤!如果今天斜率是1 / 0呢?在數學中,分母為0將被視為無效的所以這個斜率是沒有意義的,更不可能被丟進函式裡面計算,為了處理這種特殊的狀況,於是誕生了atan2。
atan2這個函數在一般情況其實跟atan沒有很大的區別,所以一般情況我們可以認為atan(y/x)等價於atan2(y, x),那什麼特殊情況呢?
就是當x = 0且y ≠ 0的時候
分母為0且分子不為0,因為atan2分成了兩個參數,就不需要面對y / 0這種異常狀況。
atan2能表現出更多象限。
atan2與atan最大的差別就是放入的資料格式,如果我們今天已知的是一個斜率,那當然就直接放入atan得到角度沒問題,但得到的結果會被限制在-π/2~π/2(含)之間,等於結果被限制在第一跟第四象限(這跟之前提到的函數概念有關,一個輸入值只能得到一個回傳值),要如何突破這個限制呢?就是當資料從斜率變成座標點時,可以透露的訊息又更多了對吧!這時候就能透過atan2來得到介於-π~π的角度了!
可能有點難理解,舉個例子來說,如果今天資料只是一個斜率-1,那我們只能放進atan最後得到了-45°(座標平面上落在第四象限),但聰明的你一定知道135°(座標平面落在第二象限)的tan值也會是-1,想得到更精確的角度就必須把資料從單純斜率變成座標點(-1, 1)然後丟進atan2(注意丟進去的順序是(y, x)),就會得到135°了!
atan:傳入值為「斜率」,回傳角度會落在-π/2~π/2(含)之間,也就是第一象限跟第四象限。atan2:傳入值為「座標」(放入時先放y再放x),回傳角度會落在-π~π(含)之間,也就是第一到第四象限都可以。知道atan2為什麼存在後來看看他如何使用吧!
了解atan2之後Math.atan2()也大同小異!
Math.atan2(y, x)
y的部分放入點座標的y
x的部分放入點座標的x
注意!這邊放的順序會是相反的,點座標(x, y)放進函式會是
Math.atan2(y, x)
他將會回傳正x軸與從(0, 0)到(x, y)的射線之間的夾角。
圖解: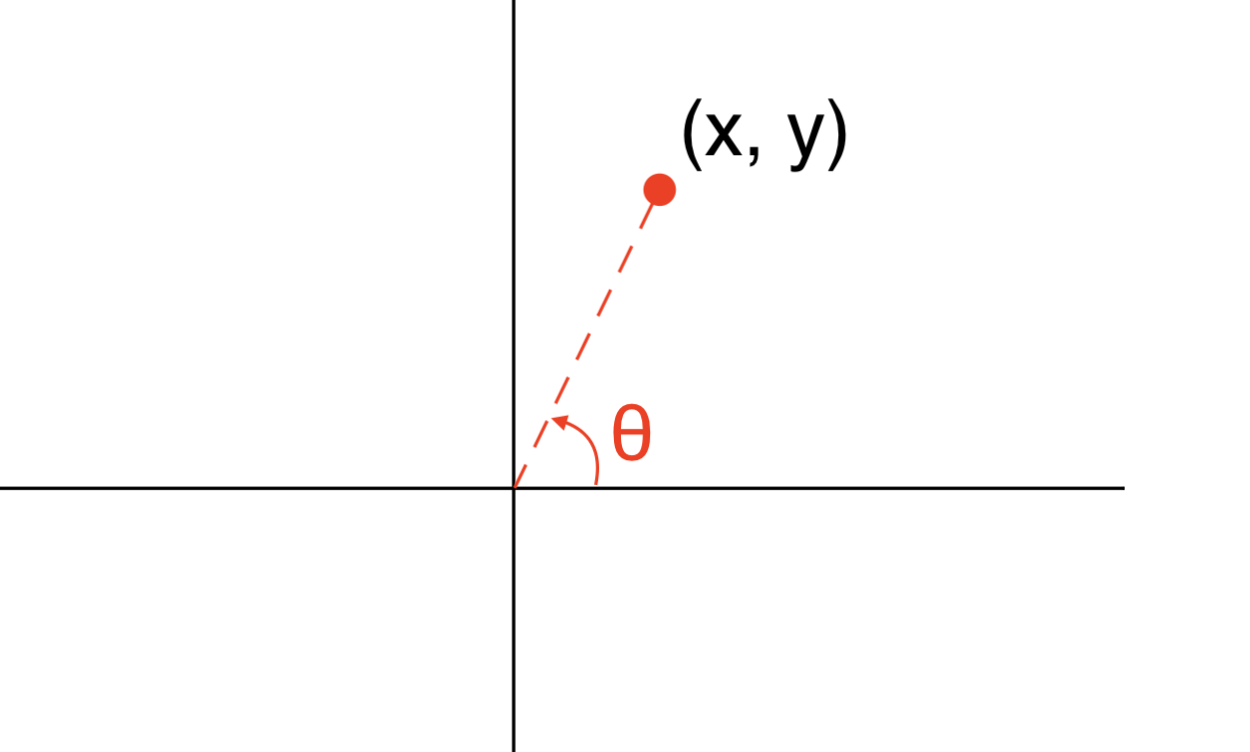
這樣應該清楚許多吧!


 ?!
?!
會不會太多?那我們今天就先到這邊吧!((不行!!!
這個函數回傳由y跟x兩個參數組成之y / x的反正切值,x與y的符號將決定結果會在哪個象限。傳統上atan2放的兩個參數順序必須是第一個放y,第二個放x。結果會是一個角度介於-π~π(含)之間。
執行以下步驟:(這邊如果本來就完全理解atan2的行為就可以跳過)
ny,值是ToNumber(y)的結果nx,值是ToNumber(x)的結果ny是NaN或nx是NaN,回傳NaN
ny是無限大:
nx是無限大,回傳π/4的近似值nx是負無限大,回傳3π/4的近似值π/2的近似值ny是負無限大:
nx是無限大,回傳-π/4的近似值nx是負無限大,回傳-3π/4的近似值-π/2的近似值ny是+0:
nx大於等於+0,回傳+0
π的近似值ny是-0:
nx大於等於+0,回傳-0
-π的近似值ny有限且不是+0或-0
ny大於+0:
nx為無限大,回傳+0
nx為負無限大,回傳π的近似值nx是+0或-0,回傳π/2的近似值ny小於-0:
nx為無限大,回傳-0
nx為負無限大,回傳-π的近似值nx是+0或-0,回傳-π/2的近似值nx有限且不是+0或-0
r,值為abs(ℝ(ny) / ℝ(nx))的反正切值nx小於-0:
ny大於+0,r設定成π - r
r設定成-π + r
ny 小於-0,r設定成-r
r的近似值終於讀完了...
講了這麼多!其實就是在判斷點(x, y)在哪個象限,如果點在一二象限,那角度會落在+0~π;如果在三四象限,角度就會落在-π~-0;然後就是處理一些無限大跟x或y為0的狀況。
對象限不了解的可以到參考資料中有維基百科可以參考
測試看看(-1, 1)能不能得到剛剛想得到135°吧!(再次提醒放入順序先y後x)
console.log(Math.atan2(1, -1) * 180 / Math.PI); //135
沒問題!!!
終於來到了最後的應用環節~再撐一下!
我們知道這個語法原來的基準點是(0, 0),那我們可以用一個技巧來改變基準點,這邊有牽扯到向量的概念,不過我想再繼續講解下去大家只會更混亂而已XDD簡單介紹一下就好:
舉例來說,如果座標平面上有兩個點(1, 1)跟(2, 3),那我想知道這兩個點的連線與x軸的夾角要怎麼做呢?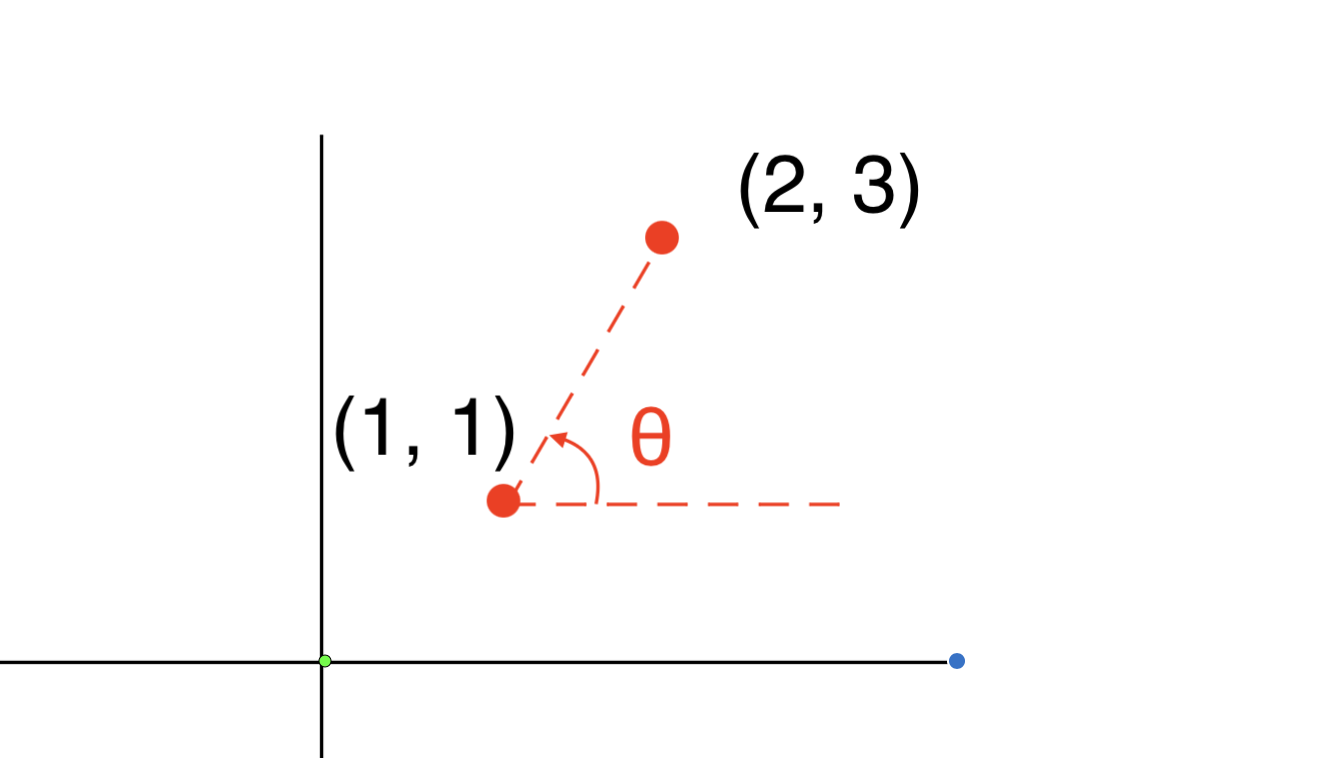
就是將後面的點扣掉前面的點(2 - 1, 3 - 1),此時的結果會是(1, 1)到(2, 3)的向量,也就是(1, 2),我們就可以想像他是以(1, 1)為基準,往右1單位、往上2單位,也就得到了「斜率」對吧!(斜率的其中一項意義:x變化1單位,y的變化量是多少)
那我們就可以想像一個二維的遊戲場景,有主角跟目標物,主角走動後就不會是在(0, 0)了對吧!就可以用這種方式來判斷主角與目標物的夾角了!
const character = {
x: 1,
y: 1
}
const target = {
x: 2,
y: 3
}
function getAngleToTarget(basic, target) {
return Math.atan2(target.y - basic.y, target.x - basic.x) * 180 / Math.PI;
}
console.log(getAngleToTarget(character, target)); //63.43494882292201
簡單設計了主角跟目標物兩個物件,裡面放著他們的x與y,我們用getAngleToTarget這個函式來取得這兩個物件之間的夾角,這個函式裡面將結果乘以180再除以Math.PI,目的是為了讓弧度轉變成角度,會比較容易觀察與理解!
從上面的例子來看,(1, 1)到(2, 3)的向量會是(1, 2),最後得到的夾角就是63.43494882292201。
終於結束了...
如果我們已知一個向量,要如何得到他與x軸的夾角呢?
寐偲,阿天卷,吐~~~
明天見。
參考資料:
維基百科-Atan2
維基百科-除以零
維基百科-象限
維基百科-向量
MDN-Math.atan2()
ECMAScript-Math.atan2()
